$$ \bbox[yellow,5px]
{
del \; A = a_{11}C_{11} + a_{12}C_{12} + ... + a_{1n}C_{1n} \\\\\\
C_{ij} = (-1)^{i+j}M_{ij}
}
$$
$$ \bbox[yellow,5px]
{
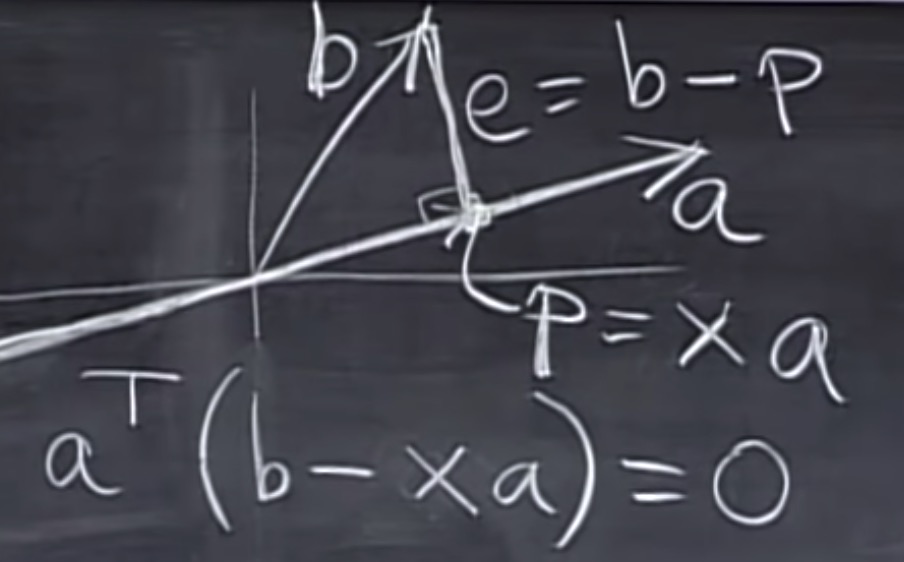
A^{-1} = \frac{1}{det\;A}C^T
}\;\;\;
\bbox[yellow,5px]
{
X_j = \frac{det B_j}{det A}, B_j 为矩阵第j列被b取代。
}
\\\\\\
\bbox[yellow,5px]
{
(u \times v) \cdot w =
\begin{vmatrix}
u_1 & u_2 & u_3 \\
v_1 & v_2 & v_3 \\
w_1 & w_2 & w_3
\end{vmatrix} = 平行六面体积
}
$$
Eigenvalues and eignevectors
$$ \bbox[yellow,5px]
{
如果 Ax = \lambda x \\
则有(A+3I)x = (\lambda + 3)x \\\\
det[A-\lambda I] = 0 \\
矩阵的迹 \; trace = \lambda_1 + \lambda_2+...+\lambda_n \\\\\\
矩阵的行列式：det A = \lambda_1 \lambda_2...\lambda_n
}
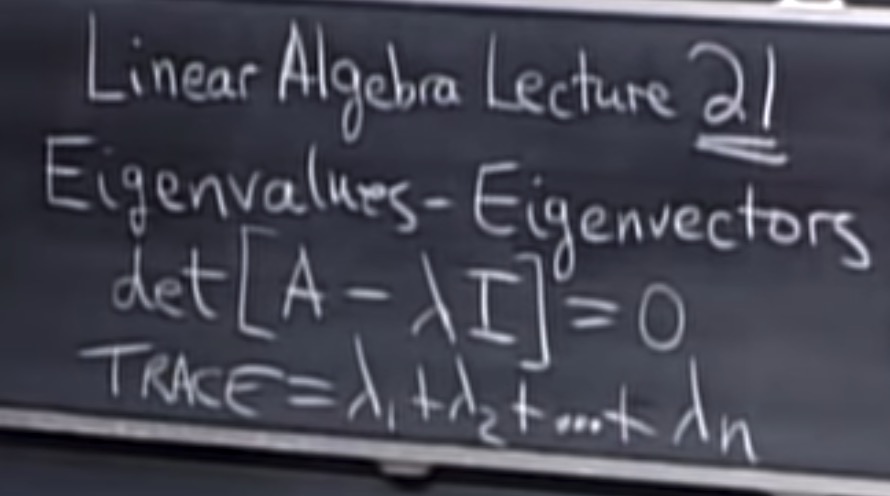
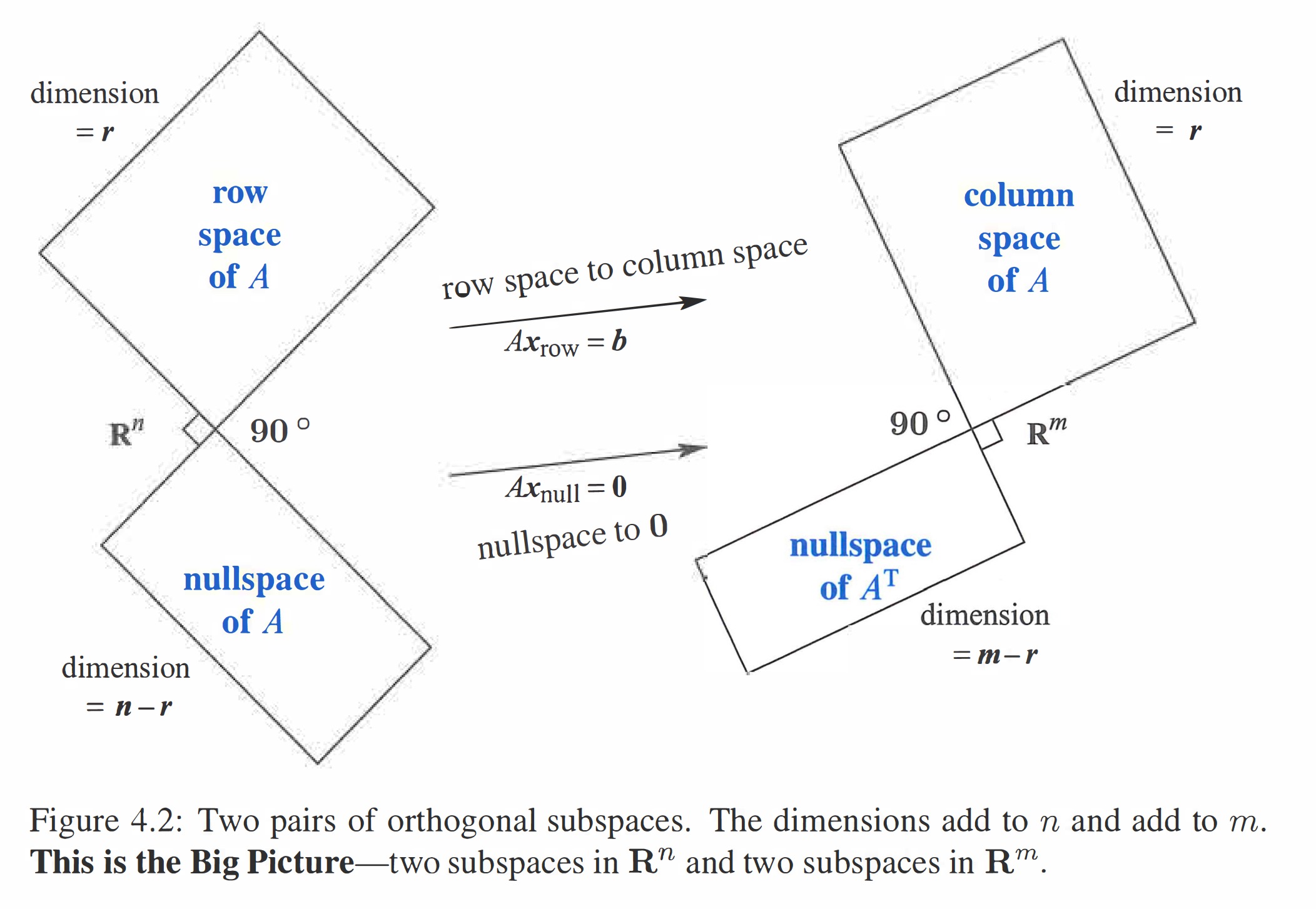
$$
向量正交和子空间正交
Ax=b及最小二乘法
