$$ \bbox[yellow,5px] { 即使不可逆矩阵，它的rank部分也是可逆的。于是导出伪逆矩阵。 } $$

双边逆（two sided inverse)

$$ AA^{-1} = I = A^{-1}A, r = m = n (全秩矩阵， full rank) $$

左逆

$$ 全列秩矩阵 r = n < m $$

零空间只有零向量，列向量全部独立。

Ax=b有唯一解或无解。 $$ (A^TA)^{-1}A^TA = I $$ 这是最小二乘的基础点。

左可逆矩阵的右逆为投影矩阵： $$ A(A^TA)^{-1}A^T = P $$

右逆

行全秩。 $$ N(A^T)= {0}, r = m < n $$ Ax=b,有解且有无穷多解

有个n-m自由变量。 $$ AA_{右}^{-1} = I \\
AA^T(AA^T)^{-1} = I $$

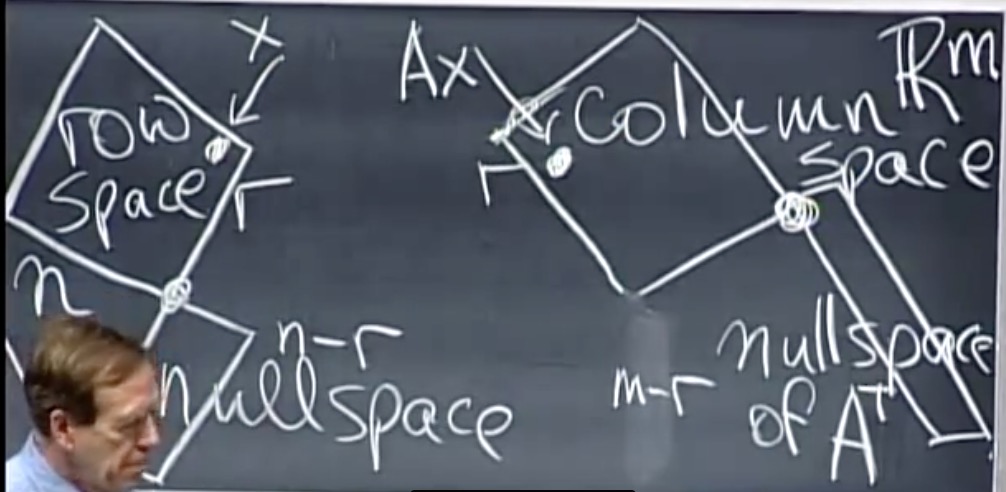
右可逆矩阵的左逆矩阵为投影矩阵: $$ A^T(AA^T)^{-1}A = P $$

伪逆矩阵

如果x$\ne$y,x, y 位于行空间， 于是Ax$<\ne$Ay.

证明：

假设Ax= Ay， 有A(x-y) = 0.

x, y, x-y都位于零空间，所以x, y是零向量。

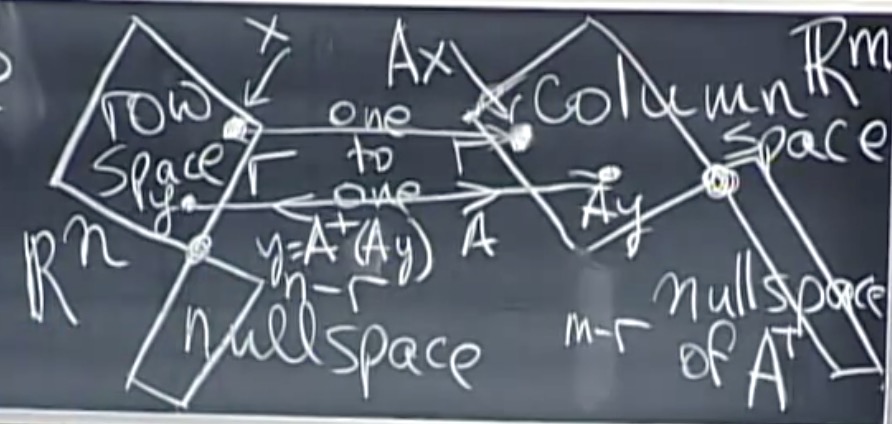
如何找到伪逆矩阵$A^+$

  1. 从SVD开始。 $$ A = U \Sigma V^T \\
    A^+ = V \Sigma^+ U^+ $$