MIT 线性代数第31讲:变更基与图像压缩
$$ \bbox[yellow,5px]
{
通过假定相互正交的向量构成正交矩阵,代替计算特征值,减少了计算量,获得了与原始矩阵接近的表达。
}
$$

有损压缩
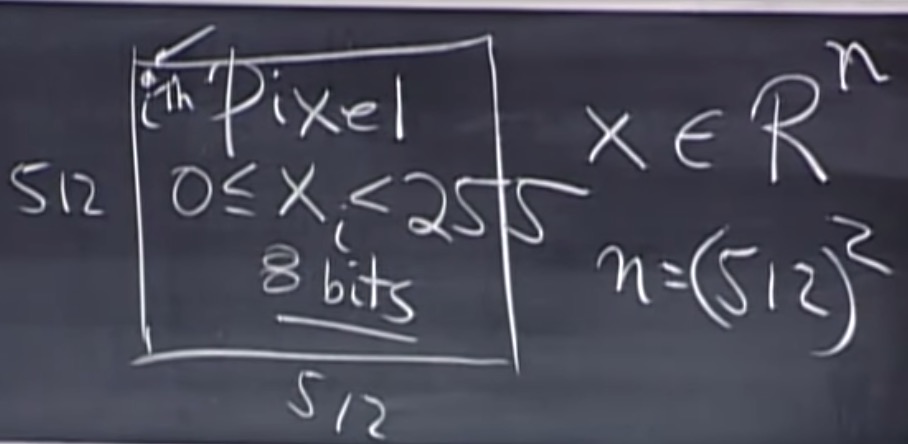
标准基:

傅里叶基:
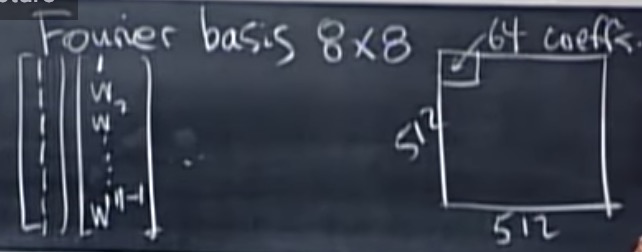
JPEG
图像被分解为8x8的块
每个块有64个像素,64个系数,64个基向量,我们在64维空间里用傅里叶向量变更基,
64个像素 P->(无损)64个系数->(有损) $\hat C$(含有不少0)
=> $\hat x = \Sigma \hat C_i V_i$
视频:
图像的序列,一张图像和上一张非常相似
图像之间高度相关,可以由上一张图像预测下一张。
Wavelets (小波)
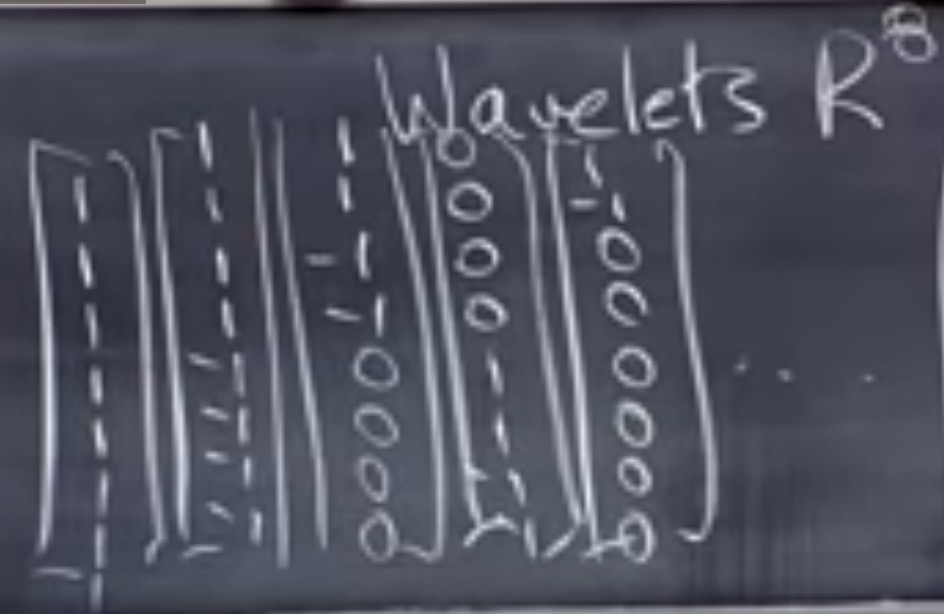
取一行8个像素:
$P=C_1 W_1 + … + C_8 W_8$: $W_i是上图的Wavelets向量。
已知P和Wi,如何求解Ci?
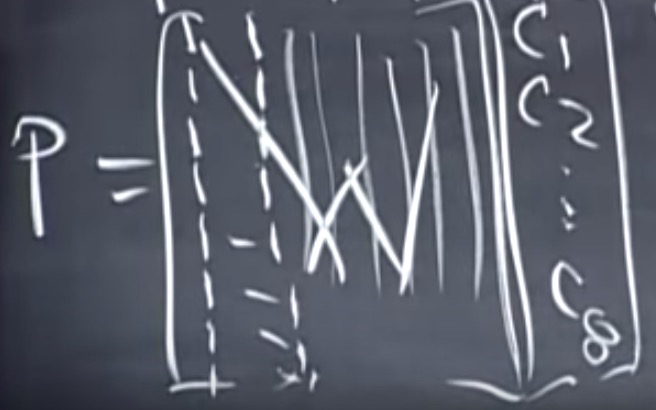
$$
P=WC \\
C=W^{-1}P
$$
好的基矩阵的要求: 1. 快:乘方和求逆快。 2. Wavelets矩阵,每个向量都相互正交,因此$W^{-1}=W^T$
- 比较少的基即可以重新生成压缩后的原始图像
基的变更
设W为新的基向量。
x = Wc
假设有现象变换矩阵T,对于u1,…, u8, 经T变换后得矩阵A
对于w1, …, w8, 经T变换后得到B。
因此,A与B相似,故有B=$M^{-1}AM$
A是什么样的矩阵:
假设使用基v1, …, v8,
我们可以从、T(v1), …, T(v8)推断T
因为每个x = c1 v1 + … + c8v8
于是 T(x) = c1T(v1)+ … + c8T(v8)
$$
T(v_1)= a_{11}v1 + ... + a_{81}v_8 \\
A =
\begin {bmatrix}
a_{11} & a_{21} & ... \\
... & ... & ... \\
a_{18} & a_{28} & ...
\end{bmatrix}
$$
假设我们的基是特征向量 $T(v_i)= \lambda_i v_i$, 那么A是什么样的矩阵?
输入是v1,输出是$\lambda_1v1$
输入是v2, 输出是$\lambda_2v2$…
因此A是主元为$\lambda_i$的对角矩阵
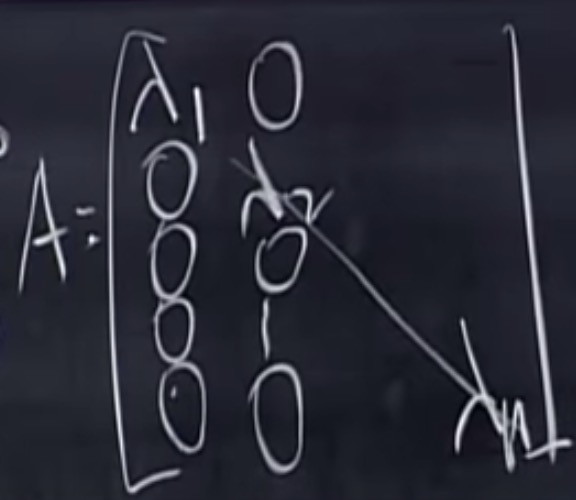
这样的矩阵是最佳矩阵, 但计算特征值需要大量计算。
因此我们选用便宜且接近的矩阵,比如小波矩阵那样。

