MIT 线性代数第30讲:线性变换和变换矩阵
$$ \bbox[yellow,5px]
{
线性变换需满足等比缩放和数值相加这两个条件。\\\\\\
可以根据变换前后的对应关系,找到变换矩阵T。
}
$$

线性变换需要满足下列条件:
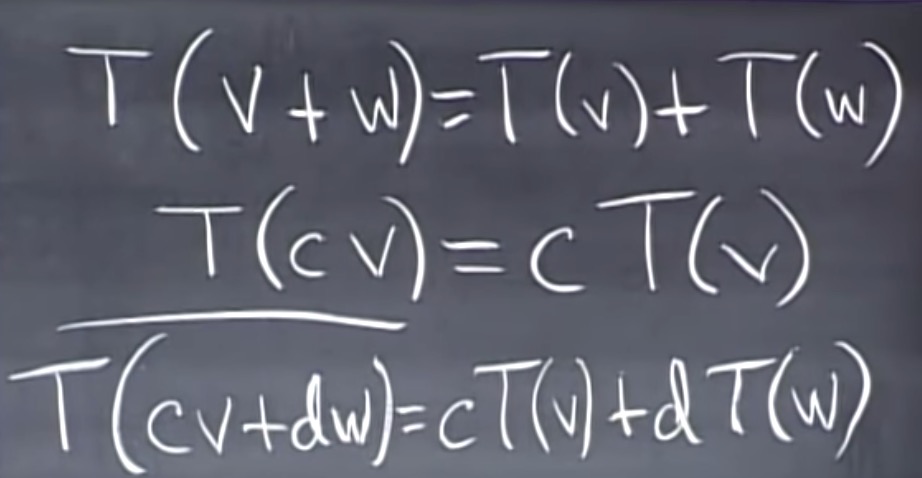
变换也称为或理解为映射(mapping)。
Ex1:
投影属于线性变换:
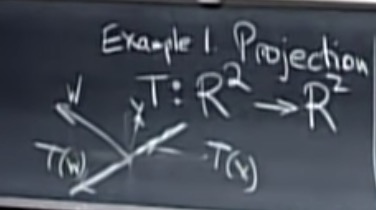
Ex2:非线性
平面移动不是线性变换:v1+v0 = T(v),因为 2v1+v0 $\ne$ 2T(v)
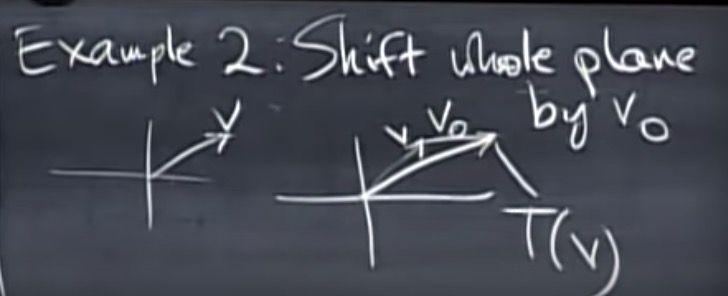
Ex3:
非线性:假设输入为-1v。。。
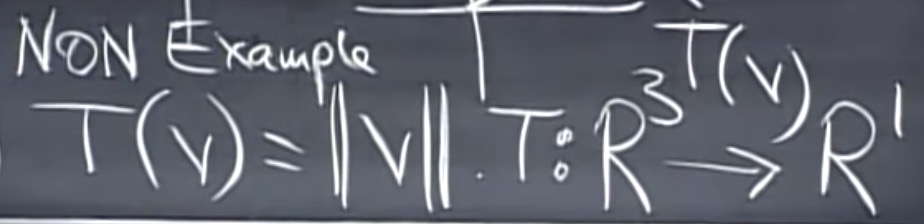
Ex:旋转:线性
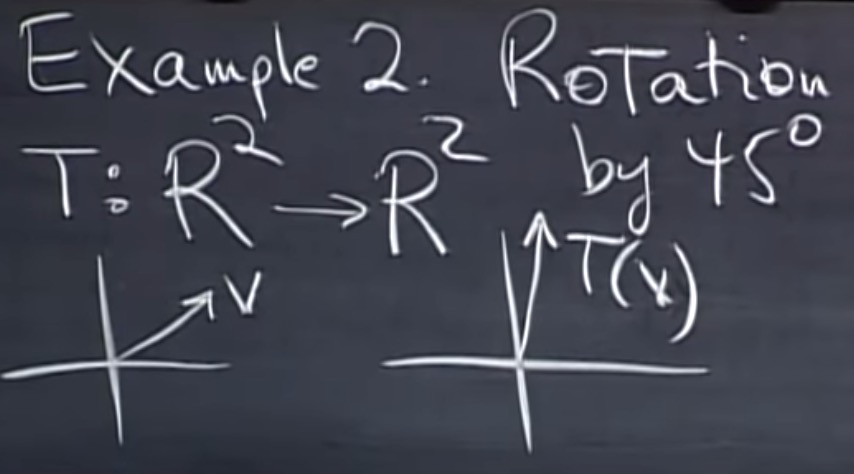
Ex T(v)=Ax : 线性!
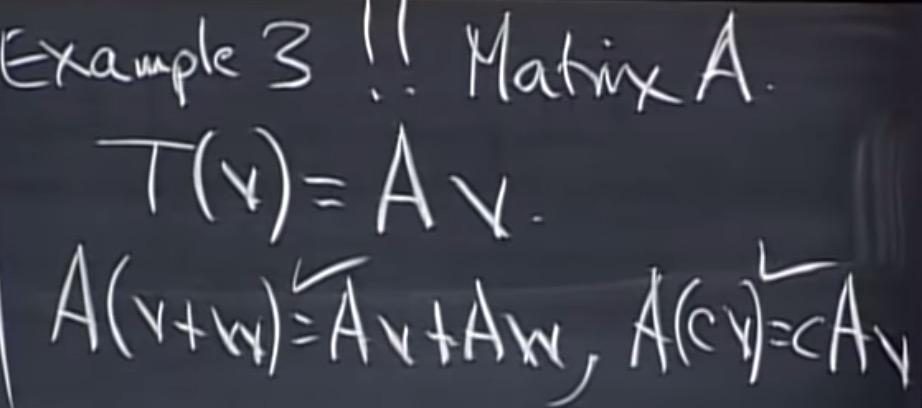
发现隐藏在变换后面的矩阵
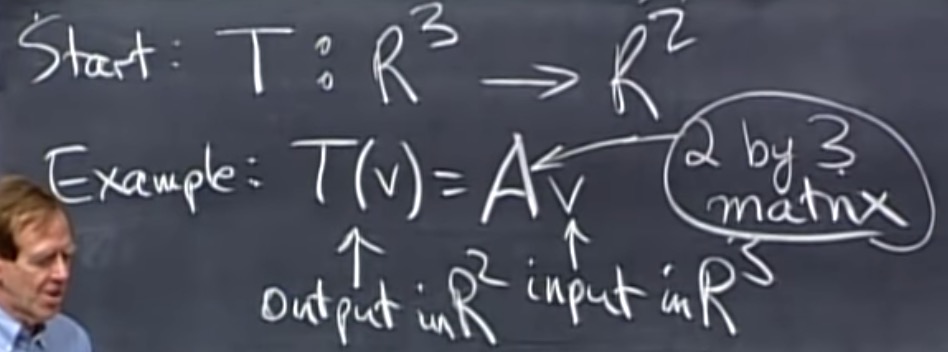
已知T(v1), T(v2), 根据线性组合,可以知道整个平面上以v1, v2为基的向量 - 前提是v1, v2相互独立

结论: 如果已知A对基的作用,即可知A对该空间所以向量的作用。
坐标源于基。
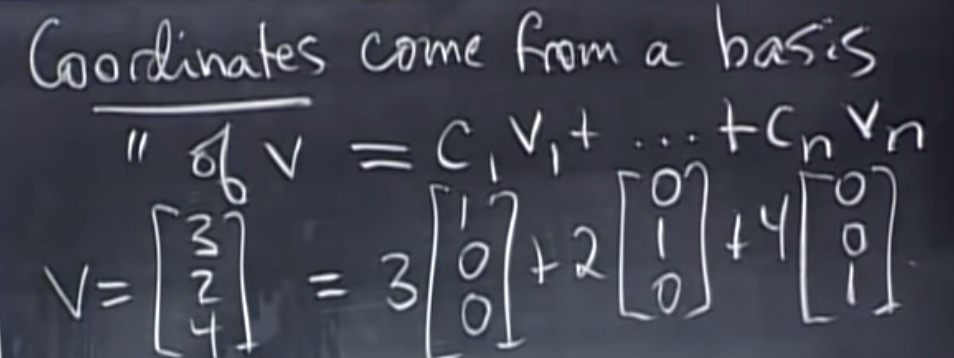
建立表达线性变换T的矩阵A
- n维空间向m维空间的变换
以特征向量构成的矩阵,生成对角矩阵,可以实施基向量方向的缩放。
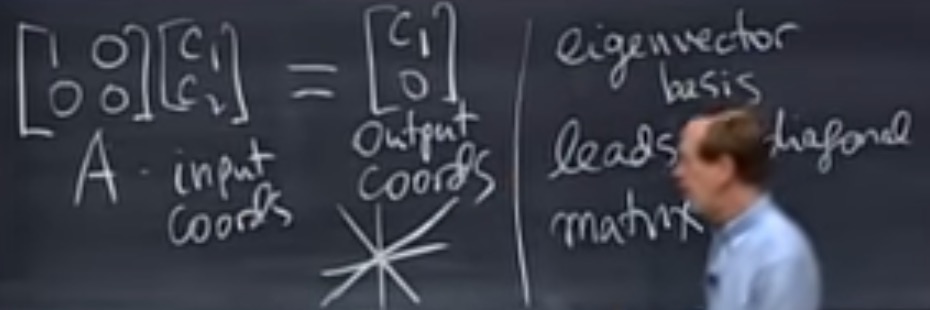
以标准基投影到45度线
找到转换矩阵A的规则:
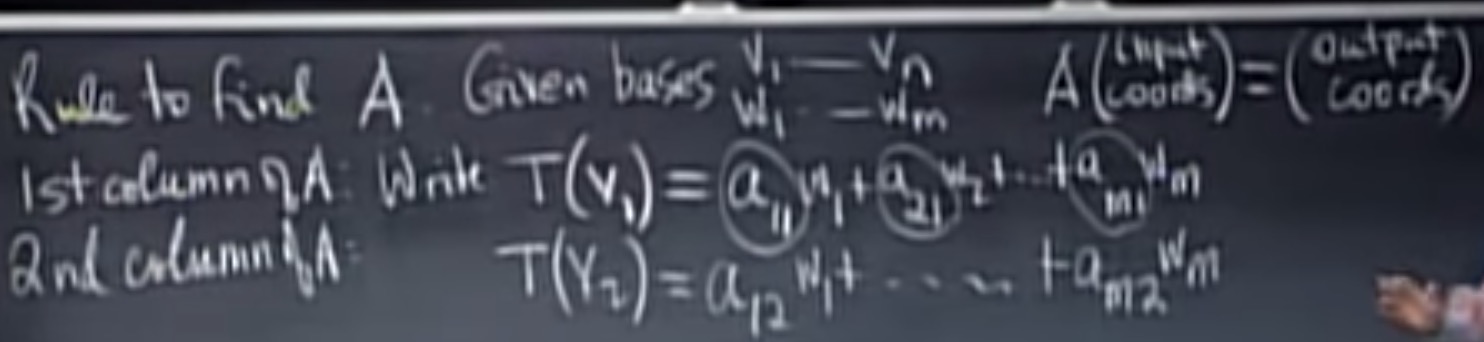
进行导数运算的矩阵:
多项式导数计算可以理解为线性变换



