$$ \bbox[yellow,5px] { SVD: A=U\Sigma V^T = u_1 \sigma_1 v_1T^+...+u_r \sigma_r v_1^T } $$

奇异值分解：singular value decomposition

引子

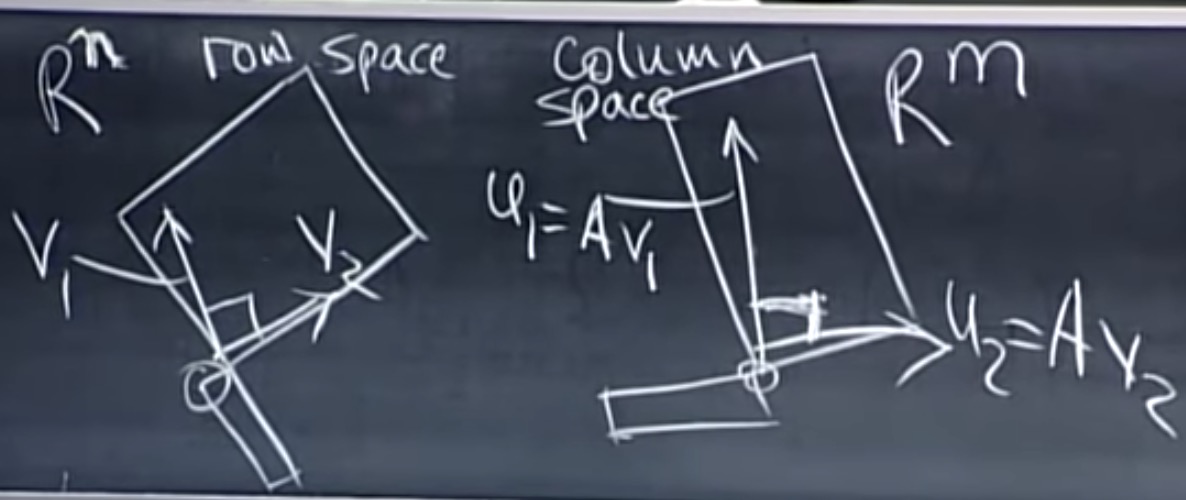
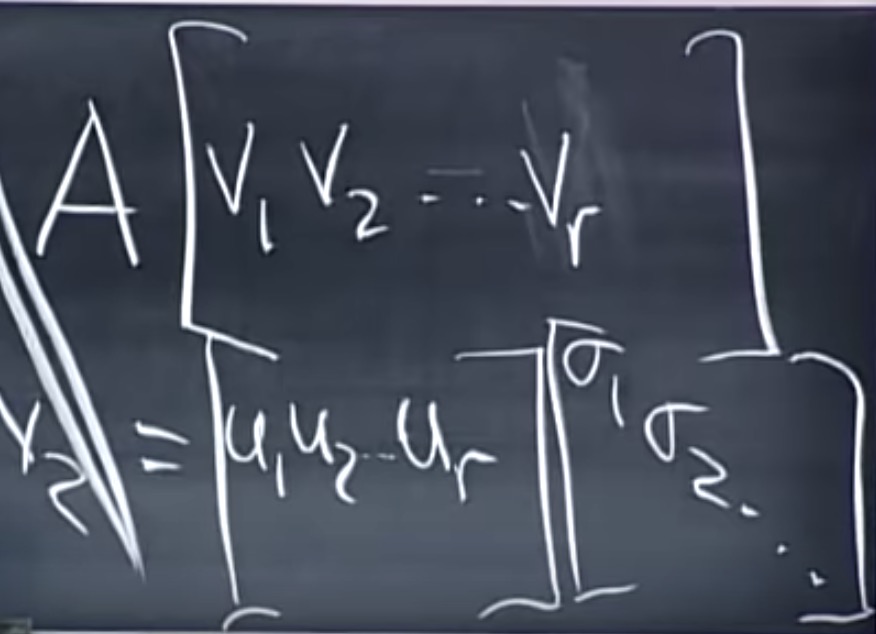
上式表述成： $$ AV = U\Sigma \\
$$ 其中$\Sigma$是对角线矩阵。

例子：

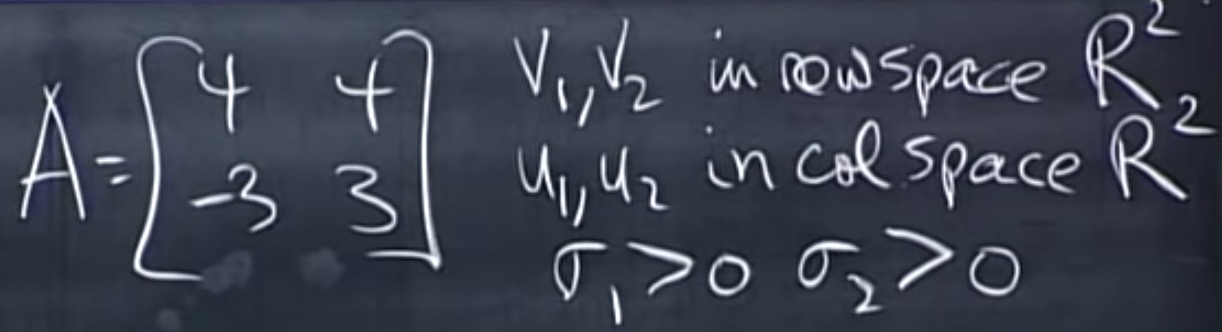
其中， u, v, $\sigma$都是规范正交向量。 $$ A = U\Sigma V^{-1} = U\Sigma V^T \\
A^TA = (V \Sigma^TU^T)U\Sigma V^T \\
= V \Sigma^T \Sigma V^2 \\
= V\Sigma^2V^T \\
= V\begin{bmatrix} \sigma_1^2 & & & \\
& \sigma_2^2 & & & \\
& & \sigma_3^2 & & \\
& & & & … \end{bmatrix} V^T $$

第一步： 计算$A^TA$

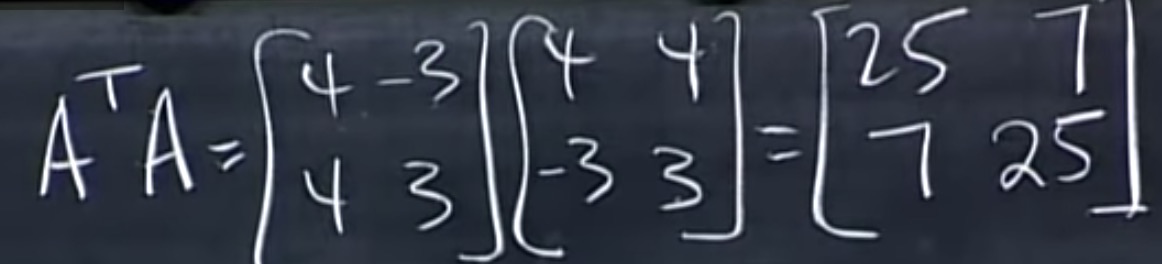
计算$A^TA$的特征值和特征向量

• 先得到特征向量，再计算特征值

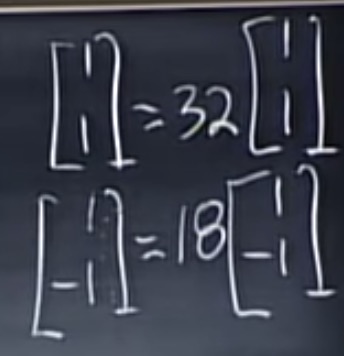
• 规范化：

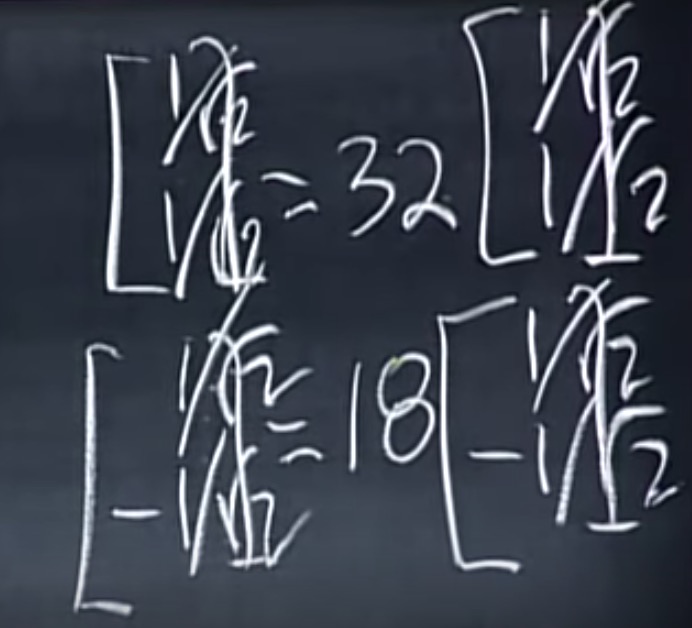
• 下面是$A, \Sigma，V^T$的值：

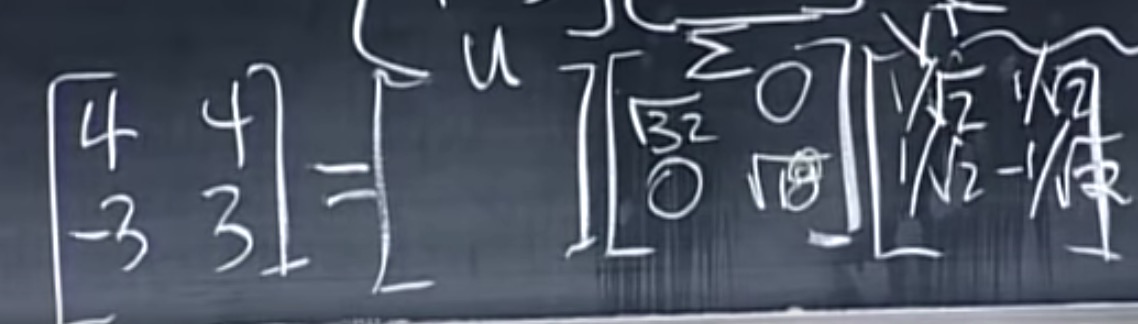
• 下面找到u：

  • $AA^T = U \Sigma V^TV\Sigma^TU^T= U\Sigma\Sigma^T U^T$
  • 
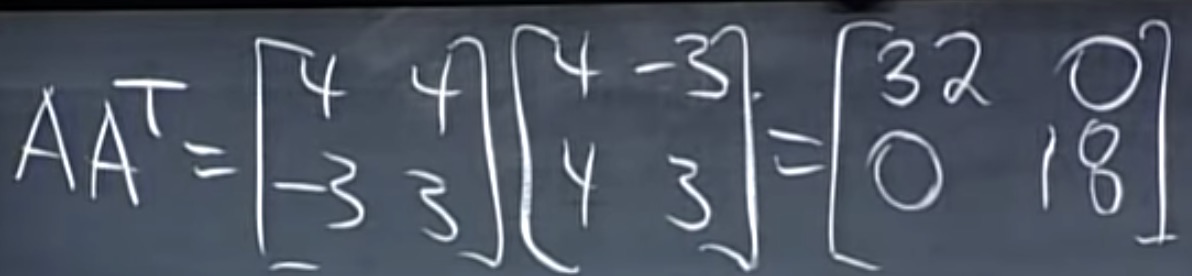
  • 上式的特征值与$A^TA$相等，因为AB的特征值=BA的特征值。

• 

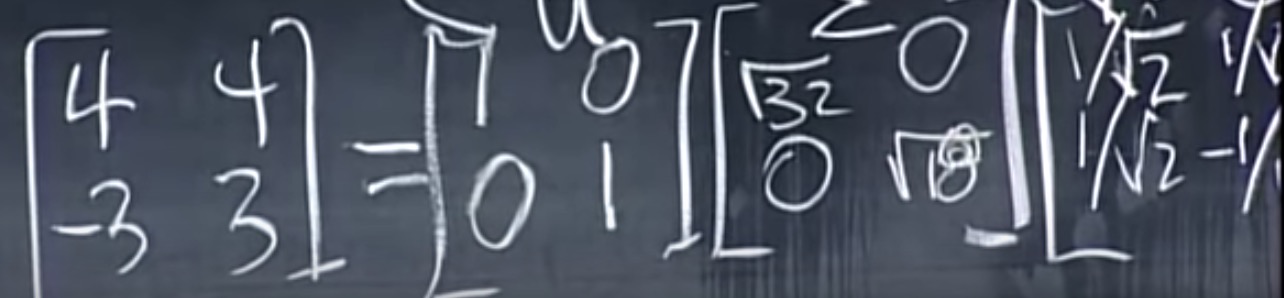
EX2：

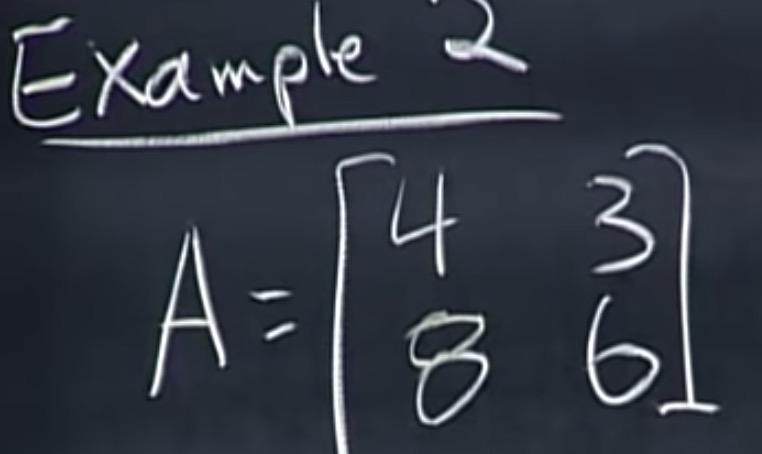
行、列空间和他们的零空间：

$$ v_1= \begin{bmatrix} 0.8 \\
0.6 \end{bmatrix} $$ 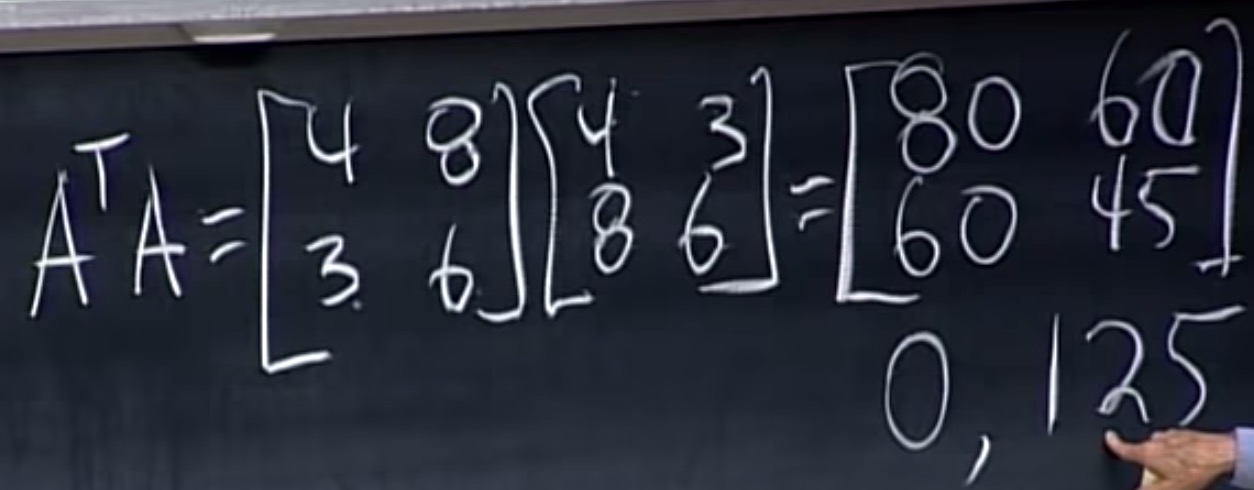上式中，已知是一维，所以一个特征值为0，又已知特征值相加为125，所以另一个特征值为125。

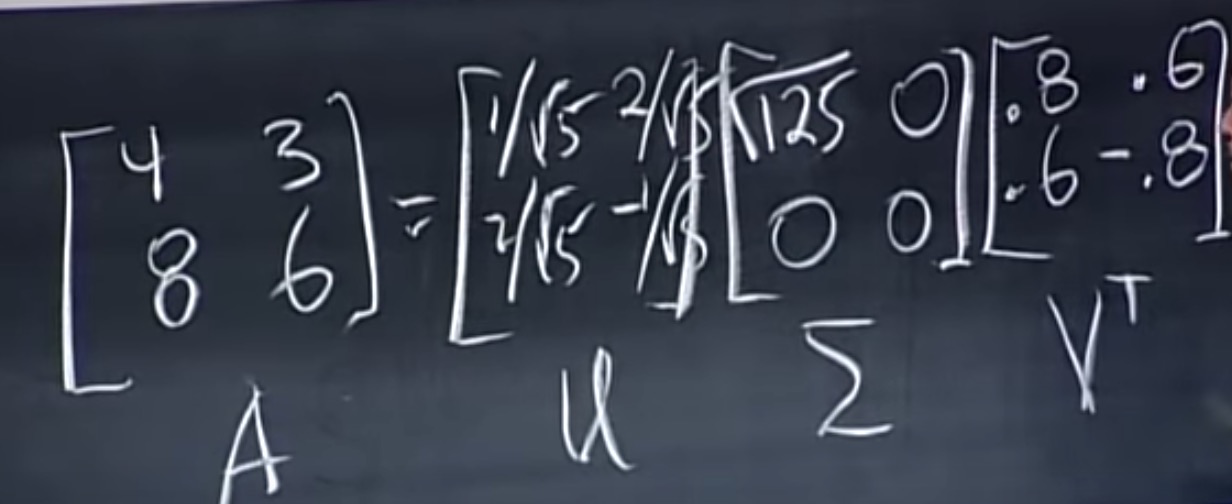
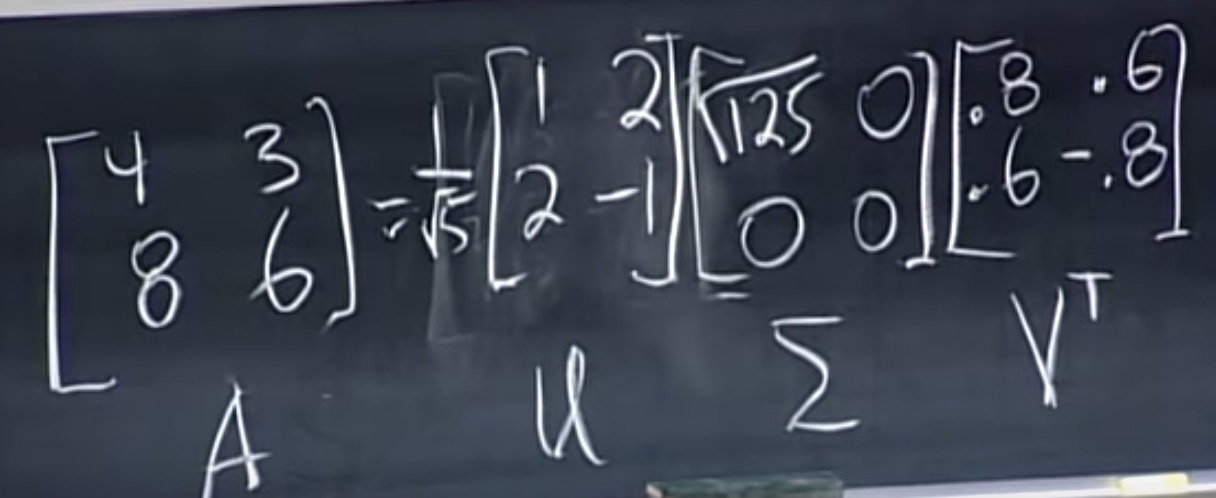
总结：

$v_1, …v_r$是矩阵行向量的正交规范基。

$u_1, …u_r$是矩阵列向量的正交规范基

$V_{r+1}, …V_n$是矩阵的零空间

$u_{r+1}, …u_m$是矩阵的左零空间。

且有：$Av_i = \sigma_i u_i$