$$ \bbox[yellow,5px] { 相似矩阵：B=M^{-1}AM \\\\\\ } $$ 乔丹型Jordan Form：可表达所有方阵，包括不能对角化的方阵

Jordan form - 又称若尔当标准型、若尔当正规型、乔登正则式。

本讲介绍相似矩阵。

再次之前简单讲一下正定矩阵。

正定矩阵

正定矩阵意味着下式成立 $$ X^TAx \gt 0 (x \ne 0) $$ 正定矩阵来自于最小二乘法、和多种物理问题。

假设A正定，它的逆同样对称、正定吗？

1. A的逆的主元：
2. A的逆的特征值：1/(矩阵的特征值)，特征值也为正。
3. 如果A、B正定。那么A+B呢？(假设$x^TAx \gt 0, xT^Bx \gt 0$)
   1. 因此$x^T(A+B)x > 0$

假设$A_{m \times n}$, 则$A^TA$为方阵，对称。 $A^TA$正定吗？

1. $x^T (A^TA)x = (Ax)^T(Ax)=\Vert Ax \Vert^2 \gt 0$
2. 如果零空间只有零向量，列向量独立，所以秩rankA=n
3. $A^TA$正定

相似矩阵

A与B相似，nxn, 非对称。则对于某些矩阵M，有$B=M^{-1}AM$

Ex:

$S^{-1}AS=\Lambda$, 根据上述定义，上式可表述为A与$\Lambda$相似。

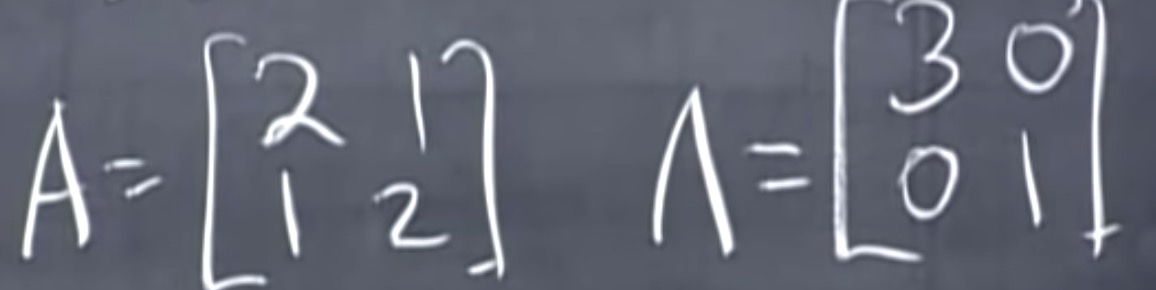
于是有$M^{-1}AM=B$: （其中M矩阵是临时编出来的）

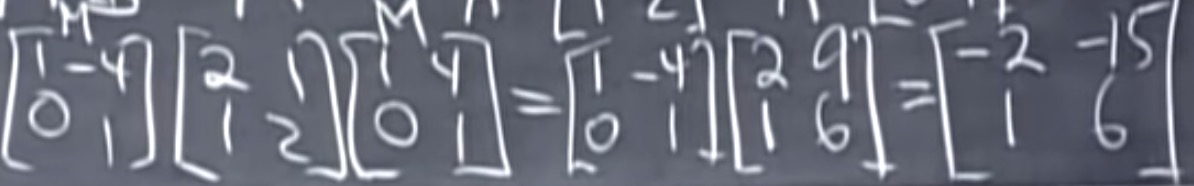
A、B、$\Lambda$有共同点，是什么？

• 他们的特征值相同。都是$\Lambda$
• 验算方法是：
  • 矩阵$\Lambda$有$\lambda_1= 3, \lambda_2 = 1$
  • 对于A， 有主元的和=2+2 = 4 = 3+1， detA = 3 = 3* 1
  • 对于B， 有主元的和=-2+6=4， detB=-2*6-(-15)*1=-12+15=3

相似矩阵的特征值相同

证明： $$ Ax = \lambda x \\
AMM^{-1}x = \lambda x \\
M^{-1}AMM^{-1}x = \lambda M^{-1} x \\
BM^{-1}x = \lambda M^{-1}x $$ 结论：B的特征向量=$M^{-1}$(A的特征向量)

一个不好的情形：$\lambda_1 = \lambda_2 = 4$

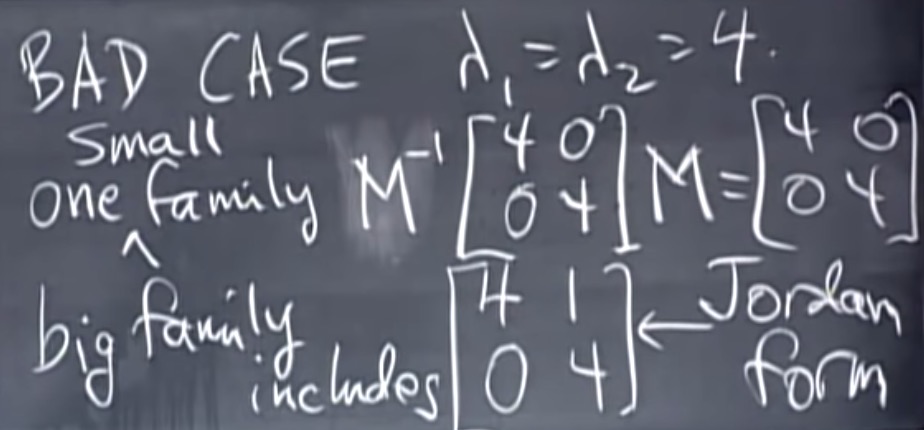
乔丹发现了每个家庭里最好看的矩阵。包括不能对角化的矩阵。最接近于对角化的矩阵就是乔丹型。

乔丹型曾经是线性代数的高潮。现在不是了， 因为对于一个通常的矩阵，发现乔丹型比较困难。

下面是一组相似矩阵的例子：

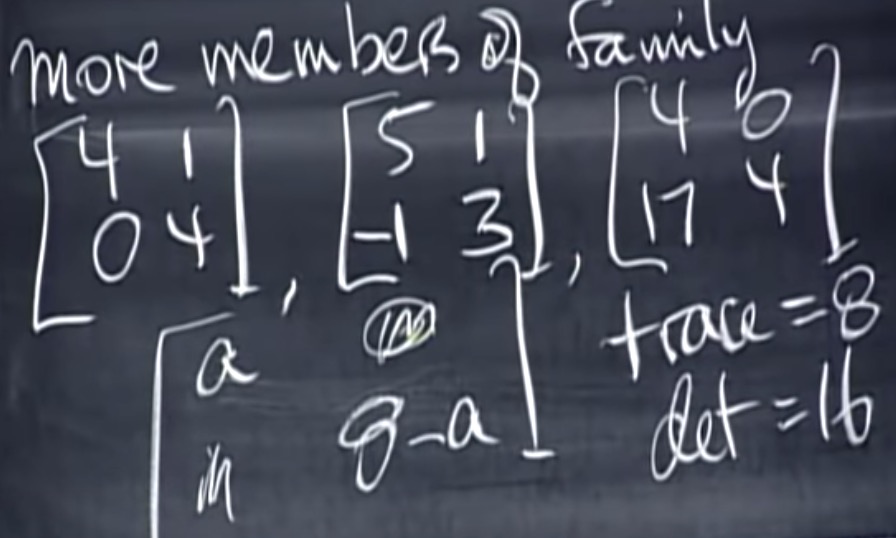
另一个例子：

$$ \lambda = 0,0,0,0 \\
有2个独立的特征值 dim N(A) = 2 $$ 每一个方形矩阵A斗鱼乔丹矩阵J相似：

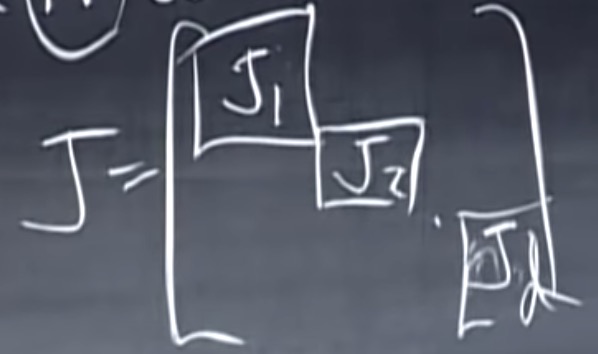
本讲未介绍乔丹型的计算方法。