$$ \bbox[yellow,5px] { 满足一下任意一条, 即为正定矩阵：\\\\\\ 1. \lambda_1 \gt 0, \lambda_2 \gt 0 - 特征值测试\\\\\\ 2. a \gt 0, ac-b^2 >0 - 行列式测试 \\\\\\ 3. 主元 a > 0, $\frac{ac - b^2}{a} \gt 0 - 主元测试 \\\\\\ 4. x^TAx \gt 0 } $$

怎样认证正定矩阵？

对于二阶矩阵： $$ A= \begin{bmatrix} a & b \\
b & c \end{bmatrix} $$

满足一下任意一条, 即为正定矩阵：

1. $\lambda_1 \gt 0, \lambda_2 \gt 0$ - 特征值测试
2. $a \gt 0, ac-b^2 >0 $ - 行列式测试
3. 主元 a > 0, $\frac{ac - b^2}{a} \gt 0$ - 主元测试
4. ==$x^TAx \gt 0​$==

依据上述描述，猜测下面矩阵缺失的元素应该是啥？

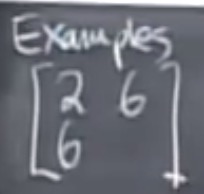
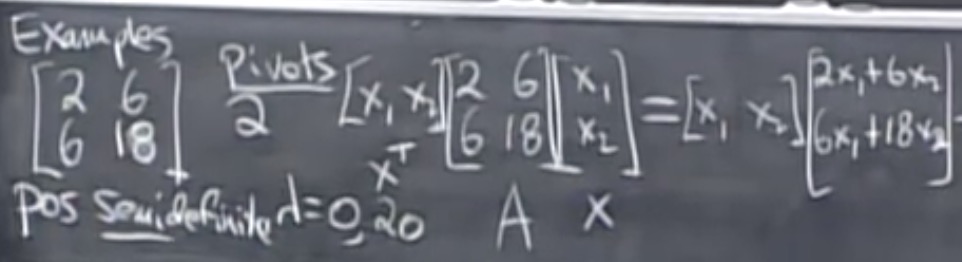
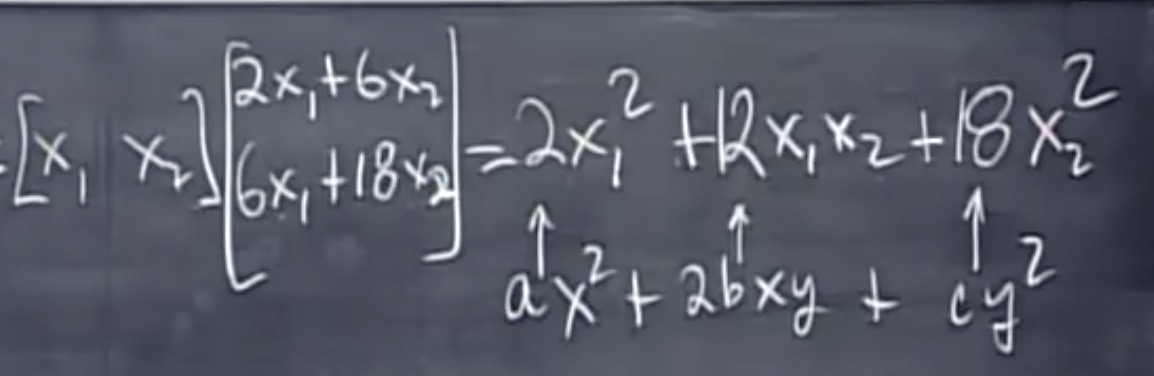
上式称为二次型 - Quardric Form

Ex1: 下述矩阵的图像是两个马鞍形，， 依赖于x, y的取值。

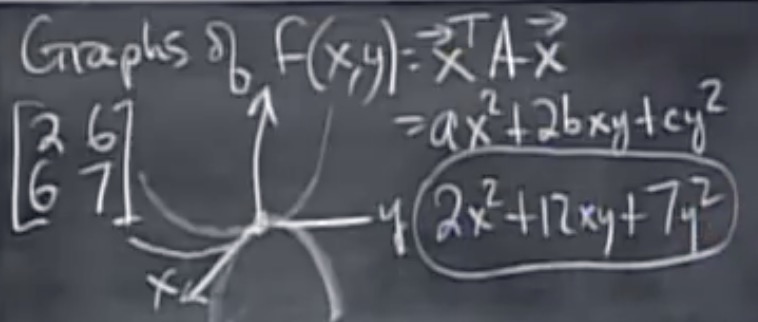
如果把上面的7换成20， 则为单纯的向上的马鞍形。

微分求最小值，有两个条件

1. 一阶导数为0， 且
2. 二阶导数 > 0: $\frac{d^2u}{dx^2} \gt 0$

矩阵极值：

$f(x_1, x_2, …,x_n)$的最小值的条件为：二阶导数的矩阵为正定

二阶导数的矩阵：

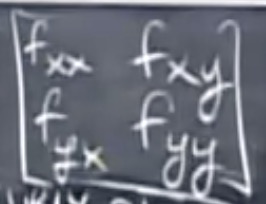
其中，$f{yx} = f{xy}$

上述矩阵：

• 子行列式为：2， 3， 4
• 主元：2，3/2, ⁴⁄₃
• 特征值:$2-\sqrt 2, 2, 2+\sqrt 2$
• $x^TAx = 2x_1^2 + 2x_2^2 + 2x_3^2 -2x_1 x_2 - 2x_2x_3 \gt 0$

paraboliad - 抛物面

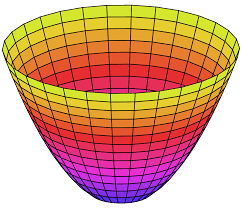
elipsoid - 椭球

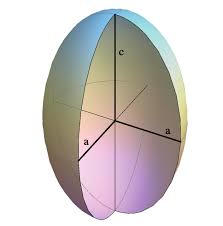
major axis - 主轴

middle axis - 中轴

minor axis - 次轴

三个轴的方向就是特征向量的方向

特征值的长度决定轴的长度

$A = Q\Lambda Q^T$