MIT 线性代数第26讲:复数矩阵;快速傅里叶变换
$$ \bbox[yellow,5px]
{
复数向量长度:Z^HZ = \Vert Z \Vert^2, 内积y^Hx,对称:A^H=A, 垂直Q^TQ=I \\\\\\
傅里叶矩阵:W=\frac{1}{\sqrt n}(W^{ij})_{i,j=0,...n-1}
}
$$

以前简单提到过复数,因为即使实数矩阵,也会有复数的特征值。
通常矩阵平方需要$n^2$次运算,通过快速傅里叶变换(FFT - fast Fourier Transform), 将矩阵平方计算缩减到$nlog_2n$次。
复数矩阵
==长度==
设有复数向量Z,$\forall Z_i \in C^n$
长度=$Z^TZ$,不再适用。
- $\bar Z_1Z_1 = \vert Z_1 \vert^2 \bar Z是Z的共轭(conjugate),$
- 因而长度计算写成$\Vert Z \Vert^2 = \bar Z^T Z$
- 例如:$$
Z=\begin{bmatrix}
1 \\
i \end{bmatrix} \\
\bar Z=\begin{bmatrix} 1 & -i \end{bmatrix} \\
\bar Z^TZ = \begin{bmatrix} 1 & -i \end{bmatrix} \begin{bmatrix} 1 \\
i \end{bmatrix} = 1+1 = 2 $$`
$\bar Z^TZ$写作$Z^HZ$,称为埃尔米特矩阵(Hermitian matrix).==内积==
- 实数内积写为$y^Tx$, 复数内积同样取共轭,写成$\bar y^Tx=y^Hx$
==对称==
- 实数写成$A^T=A$, 复数对称写成$\bar A^T=A, A^H=A$.
- Ex:
- $$A=\begin{bmatrix}2 & 3+i \\\ 3-i & 5 \end{bmatrix}$$
==垂直==
- $$q_i^Tq_j=\begin{cases}0 \; i \ne j \\\ 1 \; i = j \end{cases}$$
- $Q^HQ = I = Q^TQ$: orthogonal在复数中被方程为unitary==酉矩阵==
傅里叶矩阵
$$
F_n =
\begin{bmatrix}
1 & 1 & 1 & … & 1\\
1 & w & w^2 & …& w^{n-1}\\
1 & w^2 & w^4 & … & w^{2(n-1)} \\
… \\
1 & w^{n-1} & w^{2(n-1)} & … & w^{(n-1)^2}
\end{bmatrix}
$$
或写成:$\bbox[yellow,5px]{W=\frac{1}{\sqrt n}(W^{ij})_{i,j=0,…n-1}}$
w是特殊的数值,即$w^n=1$. $ w=e^{{i2\pi}/{n}}= cos 2 \pi / n + i sin 2 \pi / n $ .
下图介绍n=8的情形。

另一个例子, 假设n= 4, $W^4=1$
$W = e^{2 \pi i / 4}= i \\\ i^1 = i, i^2 = -1, i^3 = -i, u^4 = 1$
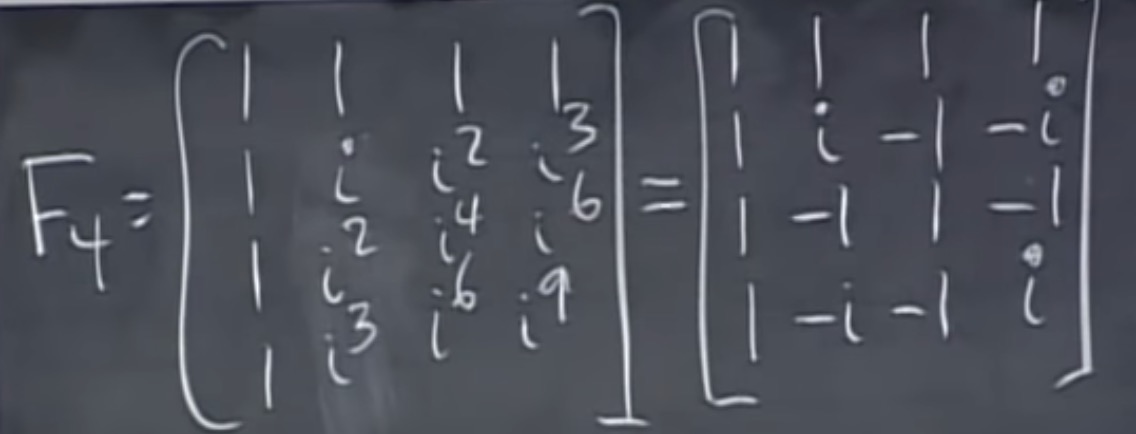
上式称为四点傅里叶矩阵。
上面的矩阵,各列向量正交。上面的列向量的和为4,所以开方为2. 所以$1/2F_4$, 则为规范正交矩阵(orthonormal)
$$F_4^HF_4 = I$$
$W_{64}^2 = W_{32}$
下图将$F_{64}化解为F_{32}$:
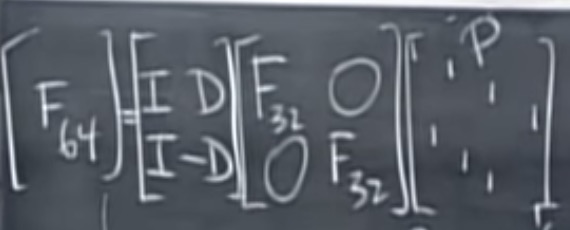
其中:
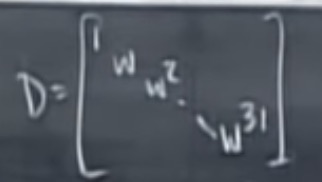
下面分解将$F_{32}分解为F_{16}的运算$:
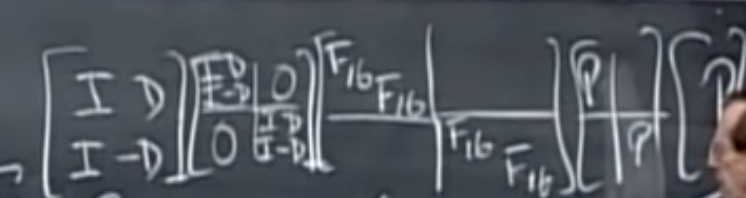
整体的运算次数:
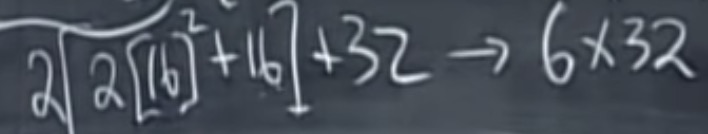
即$$1/2 \; n\,lg_2\, n$$

