$$ \bbox[yellow,5px] { 马尔科夫矩阵特征： 1. \lambda = 1为特征值 2. 所有其他的\vert \lambda_i \vert\ \lt 1 \\\\\\ 傅里叶序列： f(x) = a_0 + a_1cosx + b_1sinx + a_2cos2x + b_2sin2x+... \\\\\\ 其中：a_1 = \frac{1}{\pi} \int_0^{2 \pi} f(x)cosx \; dx } $$

马尔科夫矩阵

例子：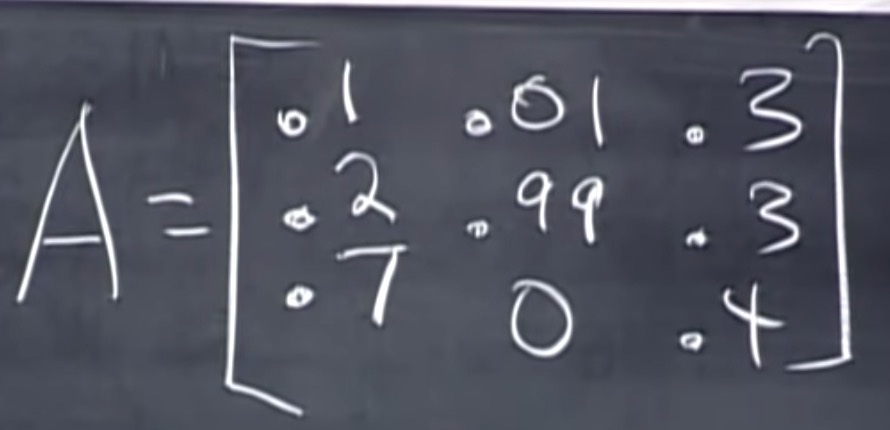

特点：

• 所有元素大于等于0
• 每个列的和为1

稳定态（stead state）

关键：

1. $\lambda = 1$ 为特征值
2. 所有其他的$\vert \lambda_i \vert\ \lt 1$

对于矩阵的平方，上述依然成立。

在微分方程中，$\lambda=0$的情况下，达到稳定状态。

在幂方情况下，$\lambda=1$达到稳定态。

所以列的数值和为1，使得1为特征值。

$$ u_k = A^ku_0 = c_1 \lambda_1^k x_1 + c_2 \lambda_2^k x_2 + … \\
\lambda_1 = 1 \\
\lambda_i \lt 0 \\
所以其余\lambda_i^k 趋近与0 \\
所以u_k = c_1x_1为稳定态。\\
\\\
特征向量：\\
x_1 \ge 0 (所有元素>0, 所以稳定状态 C_1x_1> 0) $$

计算A-1I:将A移动一个单位：

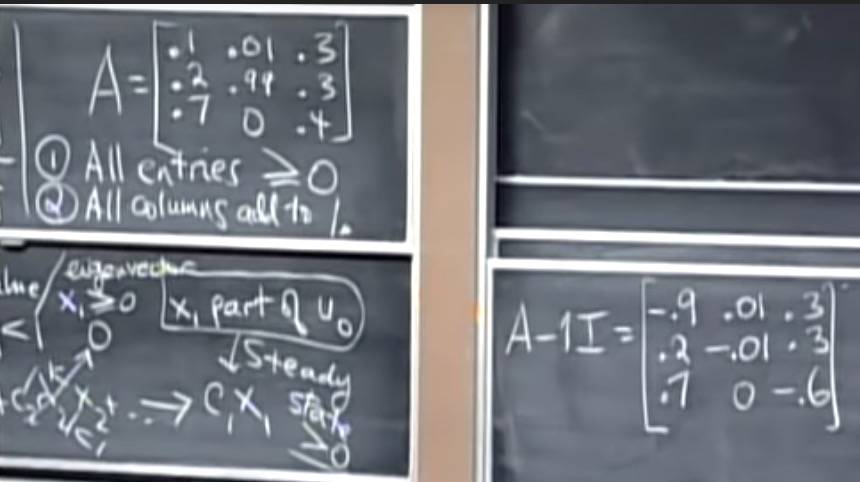
如果A-1I奇异， 则1是特征值。

为什么A-1I奇异：

1. 方法1可以计算行列式值

2. 所以A-I列的和为零，意味着A-I奇异

   1. 证明: A的三个列不独立
      1. 因为A的行不独立，A的行的线性组合和得到0：
         1. 因为(1,1,1)位于$N(A^T)$
         2. 此外x1 位于N(A)

3. A的特征值与$A^T$的特征值相等。

   1. why：

      1. $det(A-\lambda I) = 0$
      2. 上式得到$det(A^T-\lambda I)=0$ (属性10)

上式中x1 = (0.6 33 0.7),所以值都为正。

马尔科夫矩阵的由来

假设我们有矩阵A为马尔科夫矩阵(Markov matrix),则有方程

$u_{k+1} = Au_k$

Ex:

假设一个2x2的矩阵，则有两个状态。 加州和麻省的人口。矩阵告诉我们加州和麻省的人口互相迁移。这个矩阵满足列的和为0 ，所以的元素大于零。位于时刻某一年t=k+1，加州有90%的人口未迁徙，10%迁移到麻省。麻省有80%未迁徙，20%迁徙到加州：

怎样计算比方说100年后的人口情况？或者说这个矩阵的100次方？

假设人口的初始状态 k = 0：

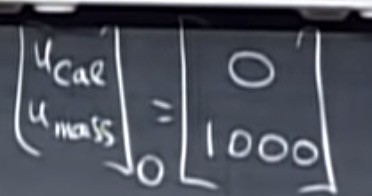
第一年过后， k = 1:

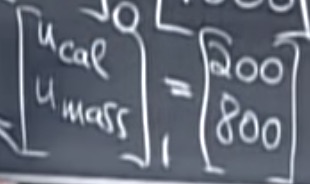
这个迁徙的稳定态，假设100年后是啥样？我们得计算特征值和特征向量。

1. 一个$\lambda = 1$
2. 另一个$\lambda$怎么计算：
   1. 根据trace：trace = 0.9+0.8 = 1.7， 所以$\lambda$=0.7
   2. 根据det= 0.9x0.8 - 0.1x0.2 = 0.7
3. 现在计算特征向量：
   1. 对角元素减去1： $$ \begin{bmatrix} 0.9 & 0.2 \\
      0.1 & 0.8 \end{bmatrix} - \begin{bmatrix} 1 & 0 \\
      0 & 1 \end{bmatrix} = \begin{bmatrix} -0.1 & 0.2 \\
      0.1 & -0.2 \end{bmatrix} \\
      \\
      解：\begin{bmatrix} -0.1 & 0.2 \\
      0.1 & -0.2 \end{bmatrix} x_1 = \begin{bmatrix} 0 \\
      0 \end{bmatrix} \\
      得到x_1 = \begin{bmatrix} 2 \\
      1 \end{bmatrix} \\
      $$ $$ 计算x_2 即带入\lambda_2: \\
      \begin{bmatrix} 0.9 & 0.2 \\
      0.1 & 0.8 \end{bmatrix} - \begin{bmatrix} 0.7 & 0 \\
      0 & 0.7 \end{bmatrix} = \begin{bmatrix} 0.2 & 0.2 \\
      01 & 0.1 \end{bmatrix} $$

$$ 解： \begin{bmatrix} 0.2 & 0.2 \\
0.1 & 0.1 \end{bmatrix} x_2 = \begin{bmatrix} 0 \\
0 \end{bmatrix} \\
得到x_2 = \begin{bmatrix} 1 \\
-1 \end{bmatrix} $$

现在计算k无穷大的情况：

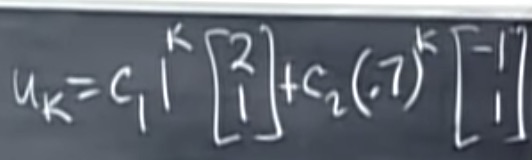
k=0的初始状态：

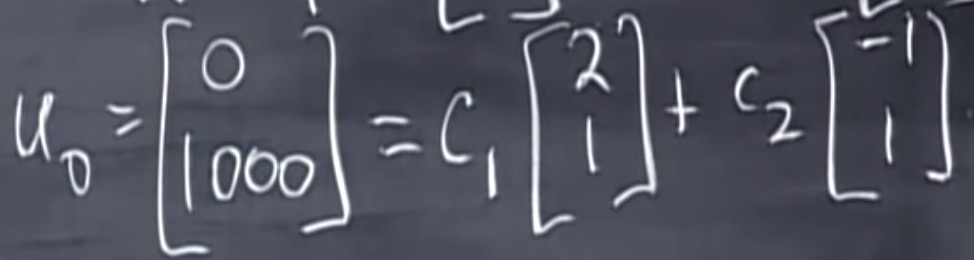
两个方程两个未知数，得到$C_1 = ¹⁰⁰⁰⁄₃, C_2 = ²⁰⁰⁰⁄₃$

傅里叶序列

特征向量

$$ x-i \ge 0 $$

单位正交基的投影（Projections with orthonomal basis)

设基向量为$q_1, …, q_n$, $\forall v = x_1q_1 + x_2q_2+ …+x_nq_n$

$$ q_1^T = x_1 q_1^Tq_q + 0 …..+ 0 \\
= x_1 q_1^Tq_q + 0 …..+ 0 \\
$$ 或者用矩阵表述

$$ v = \begin{bmatrix} q_1 & … & q_n \end{bmatrix} \begin{bmatrix} x_1 \\
x_2 \\\
… \\
x_n \end{bmatrix} X = Q^{-1}V = Q^TV \\
x1 = q_1^T $$

傅里叶序列的公式

$$ f(x) = a_0 + a_1cosx + b_1sinx + a_2cos2x + b_2sin2x+… $$

函数的叉乘是啥意思？

向量：$v^Tw = v_1w_1+…. + v_nw_n$

函数：$f^Tg = \int_0^{2 \pi} f(x)g(x)dx$

$$ \int_0^{2 \pi} sinx \; cosx \; dx = \frac{1}{2}(sinx)^2 \int_0^{2 \pi} = 0 \\
$$ $$ \int_0^{2 \pi} f(x)cosx\;dx \\
= a_1 \int_0^{2 \pi} (cosx)^2 dx = a_1 \pi \\
a_1 = \frac{1}{\pi} \int_0^{2 \pi} f(x)cosx \; dx $$

视频连接