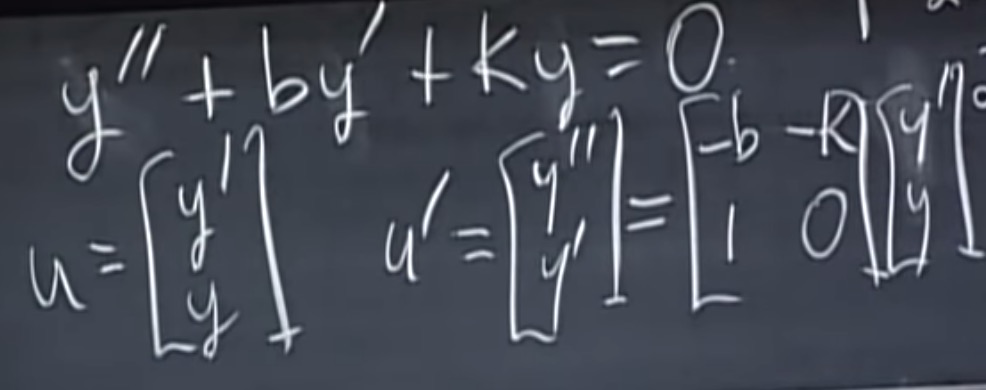MIT 线性代数第23讲:微分方程和乘方$e^{At}$
$$ \bbox[yellow,5px]
{
\frac{du}{dt}=Au \\
e^{At} = Se^{\Lambda t}S^{-1}}
$$

微分方程
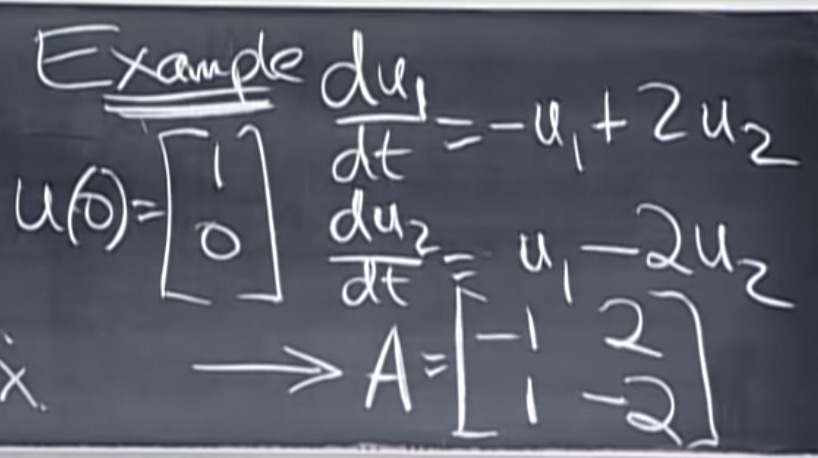
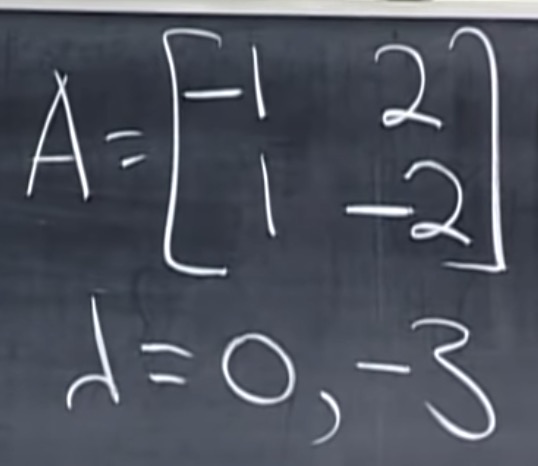
解1:这个方程奇异,所以它的一个$\lambda=0$, 它的迹(trace) = -1 + (-2) = -3. 根据trace = $\lambda_1 + \lambda_2$,得到
$\lambda_2=-3$.
解2:带入方程:
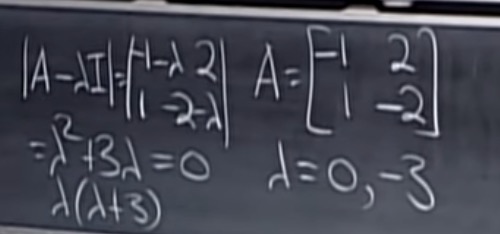

$$
v(t) = e^{\lambda t} \\
u(t) = Se^{\Lambda t}S^{-1}u(0) = e^{At}u(0) \\
e^{At} = Se^{\Lambda t}S^{-1}
$$
e的幂是什么含义?
$$
e^{At} = I + At + \frac{(At)^2}{2} + \frac{(At)^3}{6}+…+\frac{(At)^3}{n!} \\
= I + S \Lambda S^{-1} + \frac{S \Lambda^2 S^{-1}}{2}+…\\
= SS^{-1}+ S \Lambda S^{-1} + \frac{S \Lambda^2 S^{-1}}{2}+…\\
= Se^{\Lambda t}S^{-1}
$$
$$
(I-At)^{-1} = I + At + (At)^2 + (At)^3+ … \; \; \forall x: \vert x \vert \lt 1
$$
上式会不管t有多大,都会收敛。
下式如果t > 1, 将不收敛。
$$
e^{At} = Se^{\Lambda t}S^{-1} \\
e^{\Lambda t} =
\begin{bmatrix}
e^{\lambda_1t} & 0 & … & 0 \\
… & … & … & … \\
… & … & … & e^{\lambda_n t}
\end{bmatrix}
$$
上式收敛的条件是$\forall \lambda, Re \lambda \lt 0$, Re 表示实数部分。下图说明上式收敛的条件: $Re \lambda \lt 0, \vert \lambda \vert \lt 1 $

泰勒级数(Taylor Series)即用无限项连加式(级数)来表示一个函数。这些相加的项有函数在某一点的导数求得。写成公式:
$$\zeta(s) = \sum_{k=1}^\infty \frac{1}{k^s}$$
泰勒级数的几种特例:
- 几何级数$$\bbox[yellow,5px] {\frac {1}{1-x}= \displaystyle \sum_{n=0}^{\infty}x^n \; \forall x: \vert x \vert \lt 1}$$
- 二项式定理:$$(1+x)^\alpha = \sum_{n=0}^\alpha C(\alpha, n) x^n, \forall x: \vert x \vert \lt 1, \forall \alpha \in \Bbb C$$
以e为底的指数函数:$$\bbox[yellow,5px]{e^x = \displaystyle \sum_{n=0}^{\infty} \frac{x^n}{n!}}$$
以e为底的对数函数:$$ln(1+x)=\displaystyle \sum_{n=1}^{\infty} \frac{(-1)^{n+1}}{n} x^n$$
微分方程: