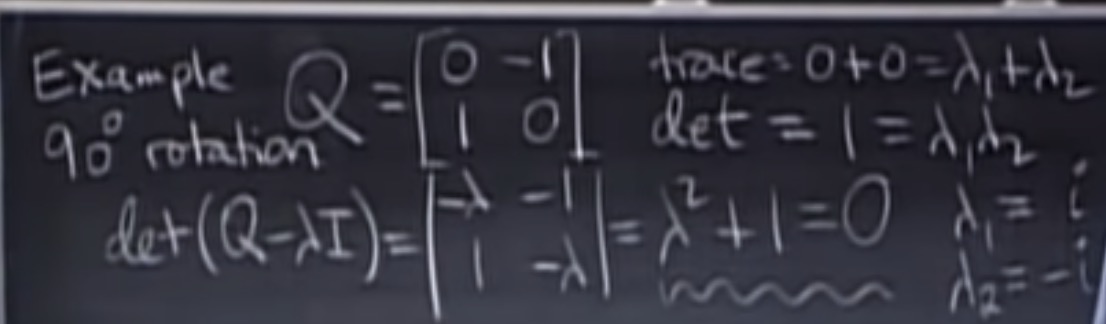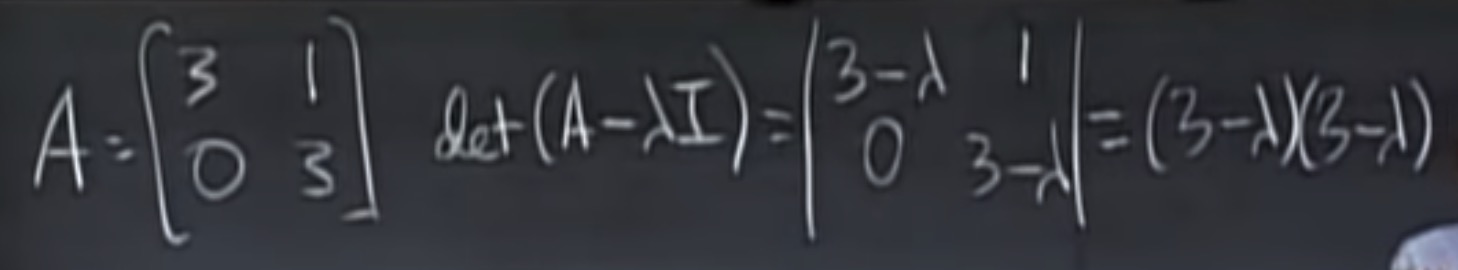MIT 线性代数第21讲:特征值与特征向量
Eigenvalues and eignevectors
$$ \bbox[yellow,5px]
{
如果 Ax = \lambda x \\
则有(A+3I)x = (\lambda + 3)x \\\\
det[A-\lambda I] = 0 \\
矩阵的迹 \; trace = \lambda_1 + \lambda_2+...+\lambda_n \\\\\\
矩阵的行列式:det A = \lambda_1 \lambda_2...\lambda_n
}
$$
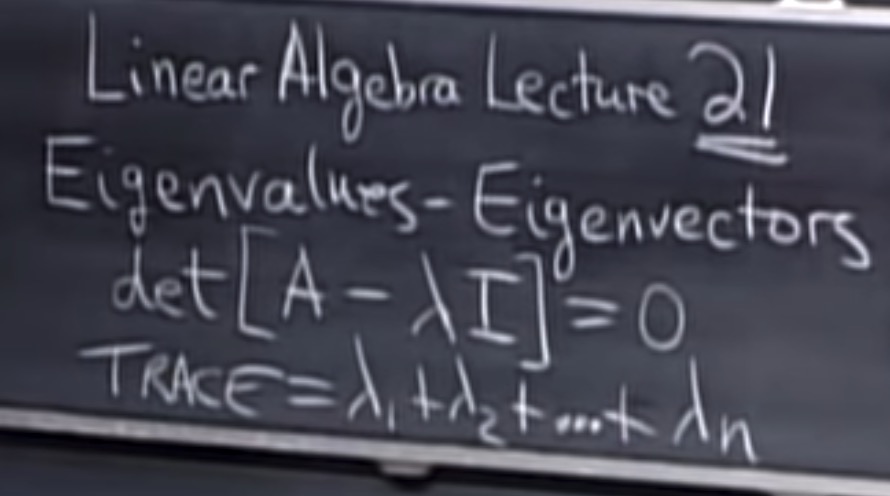
特征向量:Ax 与x平行
$$ Ax = \lambda x$$ 如果A奇异(singular, 会把非零映射到零), $\lambda = 0$为特征值
- 探讨:什么与平面平行?
- 对于任何平面上的x, Px = x,$\lambda = 1$
- 对于任何$x \bot p$: Px = 0x, $\lambda = 0$
特例:
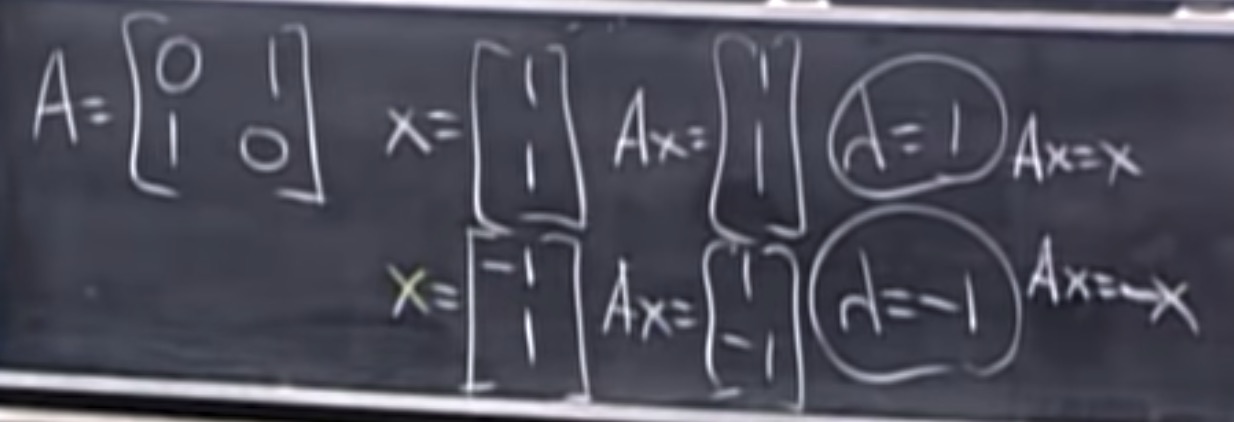
事实:矩阵A特征值的和等于斜交的和。
怎样找到特征值和特征向量?
- 怎样接$Ax=\lambda x$
- $$(A - \lambda I)x = 0 \\\\ A-\lambda I 必须为奇异矩阵 \\\ det(A-\lambda I)=0 $$
- 例子:
$$ A = \begin{bmatrix} 3 & 1 \\\\\\\ 1 & 3 \end{bmatrix} \\ det(A - \lambda I) = \begin{vmatrix} 3 - \lambda & 1 \\\\\\ 1 & 3-\lambda \end{vmatrix} = (3 - \lambda)^2 - 1 = \lambda^2 - 6\lambda - 8 = (\lambda-4)(\lambda-2) \\\\\\\ \lambda_1 = 4, \lambda_2 = 2 \\ A-4I = \begin{bmatrix} -1 & 1 \\ 1 & -1 \end{bmatrix} \\ x_1 = \begin{bmatrix} 1 \\ 1 \end{bmatrix} \\\\ A-2I = \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix} \\ x_2 = \begin{bmatrix} -1 \\ 1 \end{bmatrix} $$