MIT 线性代数第20讲:克莱姆Cramer法则、逆矩阵,体积
$$ \bbox[yellow,5px]
{
A^{-1} = \frac{1}{det\;A}C^T
}\;\;\;
\bbox[yellow,5px]
{
X_j = \frac{det B_j}{det A}, B_j 为矩阵第j列被b取代。
}
\\\\\\
\bbox[yellow,5px]
{
(u \times v) \cdot w =
\begin{vmatrix}
u_1 & u_2 & u_3 \\
v_1 & v_2 & v_3 \\
w_1 & w_2 & w_3
\end{vmatrix} = 平行六面体积
}
$$

逆矩阵
二维情况:
$$
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix}^{-1} = \frac{1}{ad-bc}
\begin{bmatrix}
d & -b \\
-c & a
\end{bmatrix}
$$
n维情况:
$$ \bbox[yellow,5px]
{
A^{-1} = \frac{1}{det\;A}C^T
}
$$
证明:
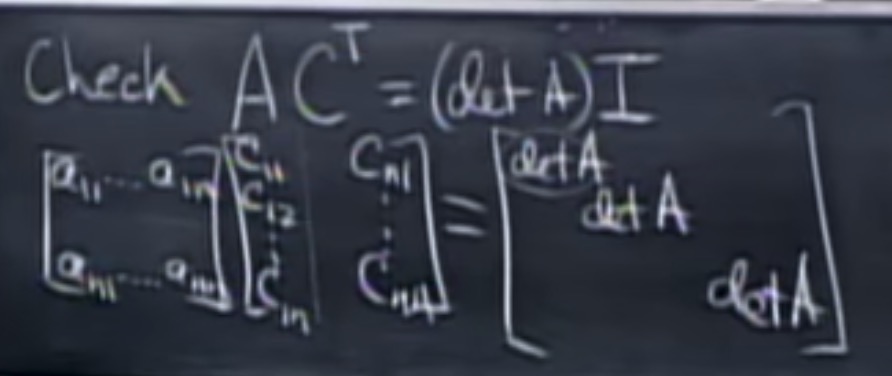
克莱姆公式:
$$ \bbox[yellow,5px]
{
Ax = b \\\\\\\\\
x = A^{-1}b = \frac {1}{det A} C^T b \\\\\\
x_j = \frac{det B_j}{det A}, B_j 为矩阵A第j列被b取代。
}
$$
(这个公式并没有实际用途,常用的做法还是消元)
行列式的值与体积
det A = 三个向量与其平行边围成的盒的体积
3维向量所围成的体积
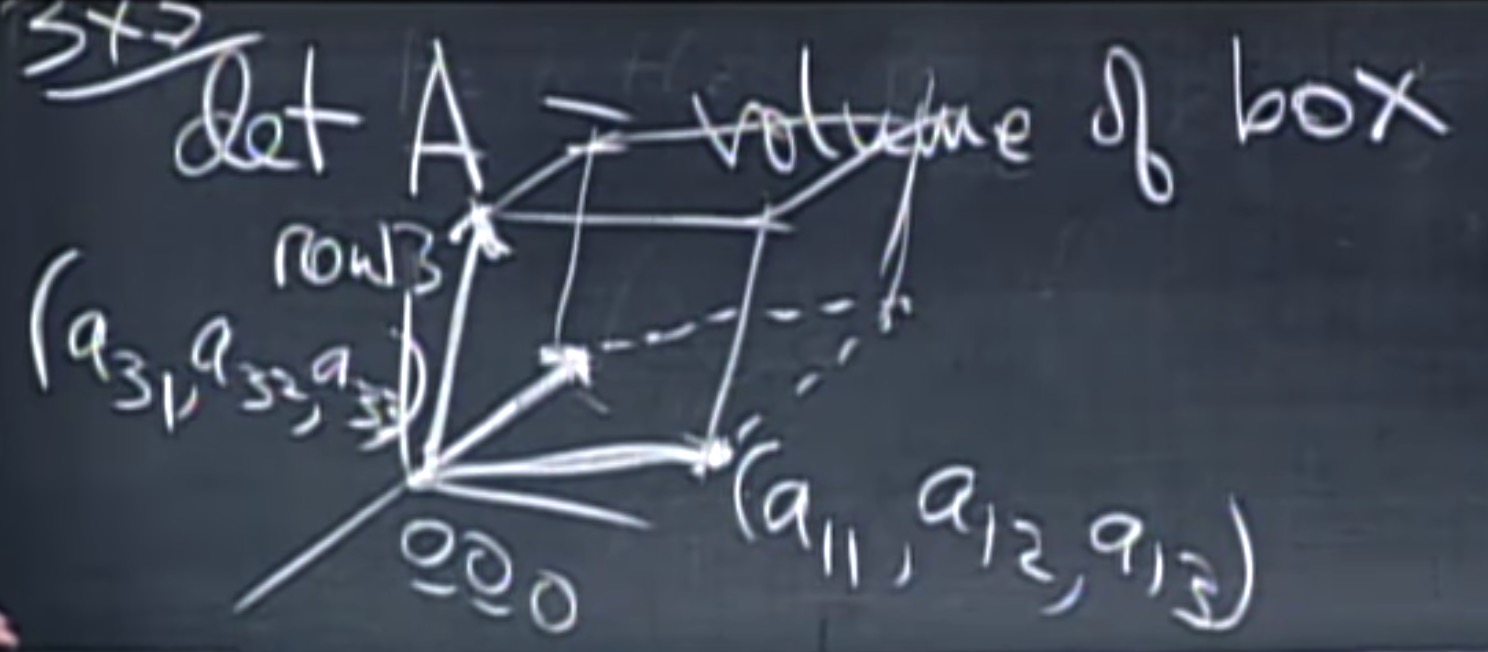
parallelogram : 平行四边形
下面的例子是平行四边形面积的计算:
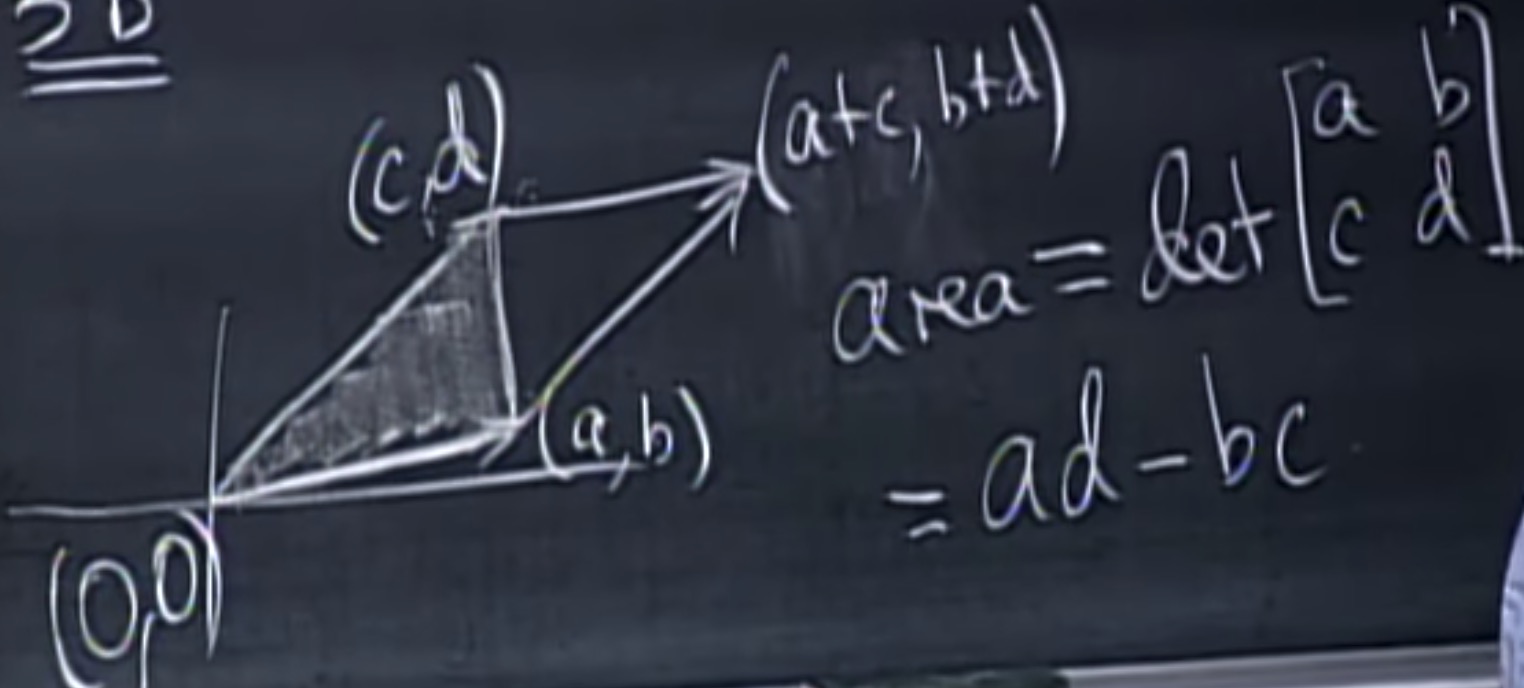
三角形的面积:
$$
三角形的面积 =
\begin{vmatrix}
x_1 & y_1 & 1 \\
x_2& y_2& 1 \\
x_3 & y_3 & 1
\end{vmatrix}
$$
triple product : 三重积
$$
(u \times v) \cdot w =
\begin{vmatrix}
u_1 & u_2 & u_3 \\
v_1 & v_2 & v_3 \\
w_1 & w_2 & w_3
\end{vmatrix}
$$
当 u, v , w共面时, $(u \times v) \cdot w $=0

