$$ \bbox[yellow,5px] { ​ del \; A = a_{11}C_{11} + a_{12}C_{12} + ... + a_{1n}C_{1n} \\\\\\ ​ C_{ij} = (-1)^{i+j}M_{ij} } $$

公式

• 根据行列式的属性，推导行列式公式 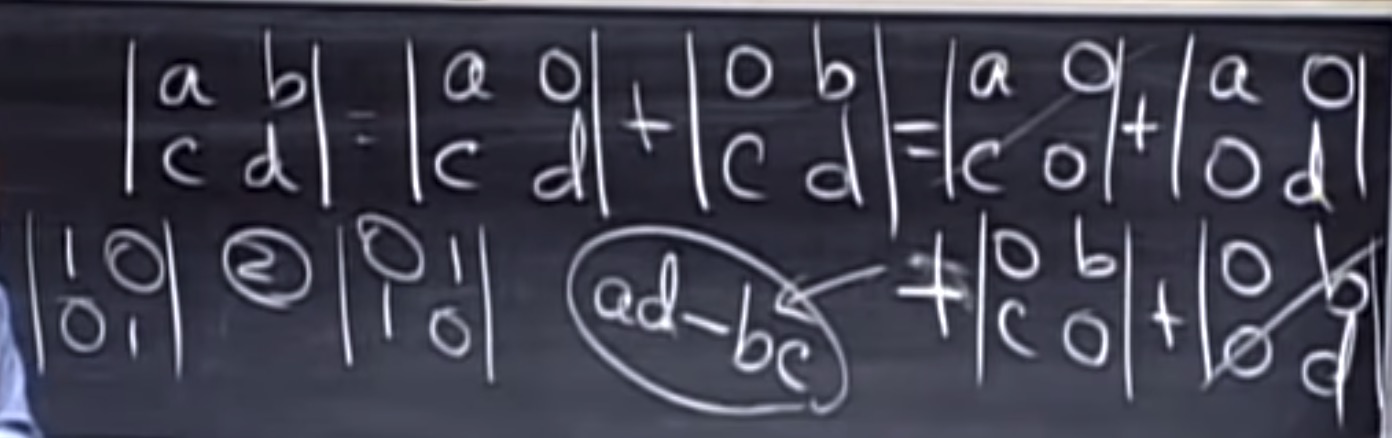3x3的情况 第一步分解出3项。。。每一个元素，行列不重复。

• 余子式

• 

$$ \bbox[yellow,5px] { ​ del \; A = a_{11}C_{11} + a_{12}C_{12} + ... + a_{1n}C_{1n} \\\\\\ ​ C_{ij} = (-1)^{i+j}M_{ij} } $$

Ex $$ A_4 = \begin{vmatrix} 1 & 1 & 0 & 0 \\\
1 & 1 & 1 & 0 \\\
0 & 1 & 1 & 1 \\\
0 & 0 & 1 & 1 \end{vmatrix} $$ 这个例子应该展示出来。