MIT 线性代数第17讲:正交矩阵和Gram-Schmidt:格拉姆-施密特正交化
Gram-Schmidt正交化提供了一种方法,能够通过这一子空间上的一个基得出子空间的一个正交基,并可进一步求出对应的标准正交基。
$$
\bbox[yellow,5px]{
q_i^T \cdot q_j =
\begin{cases}
0 , 当i \ne j\\\\\\
1, 当i = j
\end{cases}
}
$$
$$\bbox[yellow,5px] {\hat x_i = q_i^T b}$$

Orthonormal - 规范正交向量
- 定义
$$
\bbox[yellow,5px]{
q_i^T \cdot q_j =
\begin{cases}
0 , 当i \ne j\\
1, 当i = j \end{cases} } $$ - 依据上述定义, 把q向量作为矩阵的列$$Q^TQ=\begin {bmatrix} q_1^T \\\ … \\\ q_n^T \end{bmatrix}$$
于是$$Q^TQ=\begin {bmatrix} q_1^T \\\ … \\\ q_n^T \end{bmatrix}\begin {bmatrix} q_1 & … & q_n \end{bmatrix}=\begin {bmatrix} 1 & 0 & 0 \\\ 0 & 1 & 0 \\\ 0 & 0 & 1 \end{bmatrix} = I$$
结论:如果Q是方阵,那么$Q^T=Q^{-1}$
- 例1 置换矩阵
$$ Q = \begin{bmatrix} 0 & 0 & 1 \\\ 1 & 0 & 0 \\\ 0 & 1 & 0 \end{bmatrix}
Q^T = \begin{bmatrix} 0 & 1 & 0 \\\ 0 & 0 & 1 \\\ 1 & 0 & 0 \end{bmatrix} \\
Q^TQ = I $$ - 例2
$$
\begin{bmatrix}
cos\theta & -sin\theta \\
sin\theta & cos\theta \end{bmatrix} $$ 例3 $$ Q = 1/\sqrt 2 \begin{bmatrix} 1 & 1 \\\ 1 & -1 \end{bmatrix}$$
例4 Adhemer
$$ Q = 1/3 \begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & -1 & -1 & 1 \\ 1 & 1 & -1 & -1 \\\ 1 & -1 & -1 & 1 \end{bmatrix}$$例5
$$ Q = 1/3 \begin{bmatrix} 1 & -2 & 2 \\ 2 & -1 & -2 \\ 2 & 2 & 1 \end{bmatrix}$$
规划正交向量Q的优点
向列空间投影 $ P = Q(Q^TQ)^{-1}Q^T = QQ^T = I { 当Q为方阵}$
因此投影方程$A^TA \hat x = A^T b $可以简化成:
$Q^TQ \hat x = Q^T b $,得到
$\hat x = Q^T b $或者写成$$\bbox[yellow,5px] {\hat x_i = q_i^T b}$$
将独立向量转化成规划正交向量 - 格拉姆-施密特
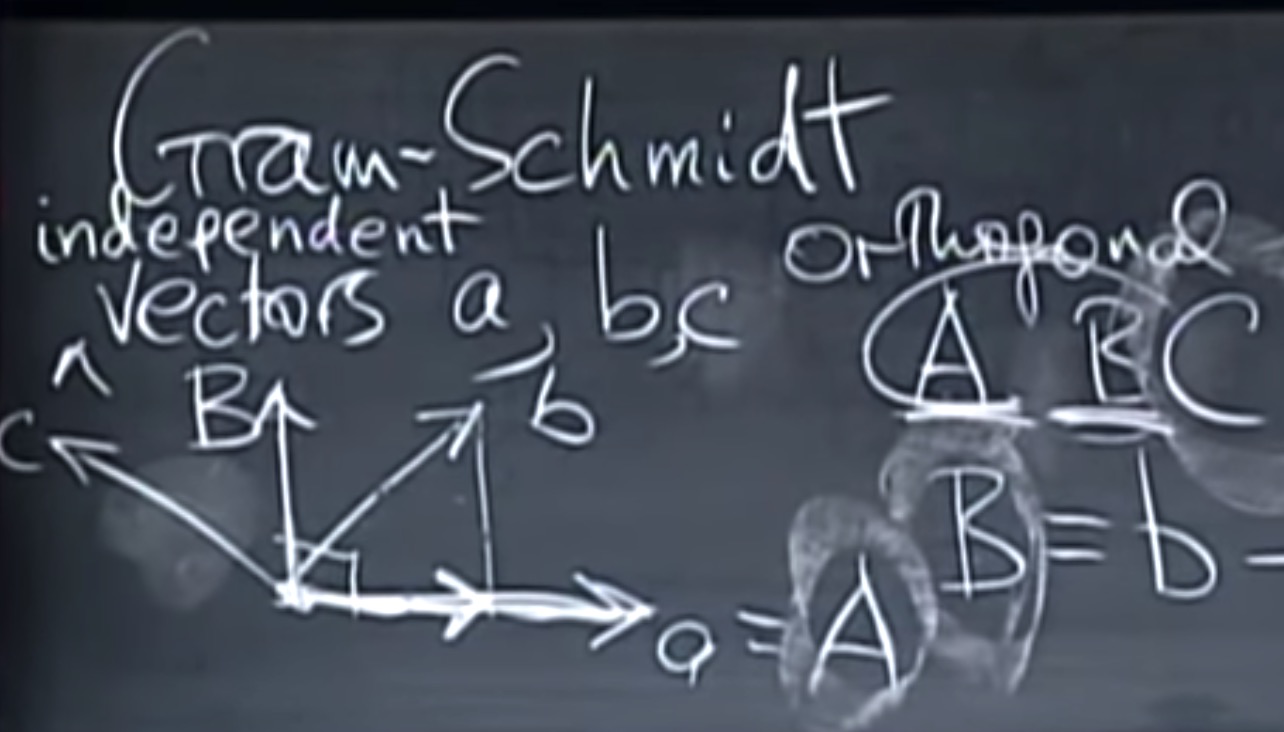
如图
$$
q_1 = \frac{A}{\Vert A\Vert} \\
q_2 = \frac {B} {\Vert B \Vert} \\
q_3 = \frac {C} {\Vert C \Vert}
$$
$$
a = A \\
B = B - \frac {A^Tb}{A^TA}A
$$
$$
由于A \bot B, 所以应该有A^TB = 0 \\
A^TB = A^T(b- \frac {A^Tb}{A^TA}A) = A^Tb - A^T \frac {A^Tb}{A^TA}A = A^Tb-A^Tb = 0
$$
现在找到C垂直于A和B, 也就是C减去A方向的分量和B方向的分量:
$$
C = c - \frac{A^Tc}{A^TA}A - \frac {B^Tc}{B^TB}B
$$
例题:格拉姆-施密特方法计算单位正交矩阵
$$
a = \begin{bmatrix}
1 \\
1 \\
1
\end{bmatrix}
b = \begin{bmatrix}
1 \\
0 \\
2
\end{bmatrix} \\
B = B - \frac {A^Tb}{A^TA}A =
\begin{bmatrix}
1 \\
0 \\
2
\end{bmatrix} - \frac{3}{3}
\begin{bmatrix}
1 \\
1 \\
1
\end{bmatrix} =
\begin{bmatrix}
0 \\
-1 \\
1
\end{bmatrix}
$$`
检查$A \bot B:
A^TB =
\begin{bmatrix}
1 & 1 &1
\end{bmatrix}
\begin{bmatrix}
0 \\
-1 \\
1
\end{bmatrix} = 0, 正确
$
$$
最终得到单位正交矩阵 Q =
\begin{bmatrix}
q_1 & q_2
\end{bmatrix} =
\begin{bmatrix}
\frac{A}{\Vert A \Vert} & \frac{B}{\Vert B \Vert}
\end{bmatrix} =
\begin{bmatrix}
\frac {1}{\sqrt 3} & 0 \\
\frac {1}{\sqrt 3} & \frac{-1}{\sqrt 2} \\
\frac {1}{\sqrt 3} & \frac{1}{\sqrt 2}
\end{bmatrix}
$$
A=QR的因式分解
上面我们有a,b, c构成的矩阵A用Gram-Schmidt方法计算得到向量为q1, q1, q3的单位正交矩阵。因此, 一定有某个矩阵是的A=QR。
$$
A =
\begin{bmatrix}
a & b & c
\end{bmatrix} = QR =
\begin{bmatrix}
q_1 & q_2 & q_3
\end{bmatrix}
\begin{bmatrix}
q_1^Ta & q_1^Tb & q_1^c \\
& q_2^Tb & q_2^b \\
& & q_3^c
\end{bmatrix}
$$
单位正交矩阵对最小二乘法的简化
A = QR 推得
$
Q^TA = Q^TQR => R = Q^TA \\
A^TA = (QR)^TQR = R^TQ^TQR = R^TR \\
最小二乘法方程:A^TA \hat x = A^Tb , 带入上式得到R^TR \hat x = R^TQ^Tb, 最终得到\\
R \hat x = Q^Tb
$
$$
\bbox[yellow,5px]
{
最小二乘法:R \hat x = Q^Tb 或者 \hat x = R^{-1}Q^Tb
}
$$

