MIT 线性代数第16讲:投影矩阵和最小二乘
线性回归的计算
$P = A(A^TA)^{-1}A^T$
$$A^TAx = A^Tb$$
复习:

$P = A(A^TA)^{-1}A^T$
b = p+e
p=Pb
e = b - p = b - Pb = (I-P)b
(因为b = e + Pb, 所以e= b-Pb = (I-P)b)
$$
e = b - p \\
e垂直于a \\
A^T(b-p) = 0 \\
A^Tp = A^Tb \\
A^TA \hat x = A^T b
$$
例题
线性拟合的问题是最小化 $\Vert e \Vert^2 = \Vert Ax - b \Vert^2 = e_1^2 + e_2^2 + e_3^2$
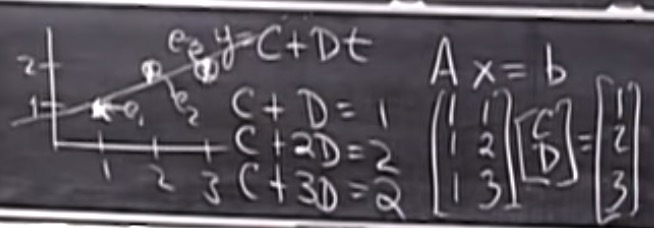
不处理偏离的的值(outlier)
$$A^TA = \begin{bmatrix}
1 & 1 & 1 \\
1 & 2 & 3
\end{bmatrix}
\begin{bmatrix}
1 & 1 \\
1 & 2 \\
1 & 3
\end{bmatrix}=\begin{bmatrix}3 & 6 \\\ 6 & 14 \end{bmatrix}$$
$$ A^Tb = \begin{bmatrix}
1 & 1 & 1 \\
1 & 2 & 3
\end{bmatrix}
\begin{bmatrix}
1 \\
2\\
2
\end{bmatrix}=\begin{bmatrix}5 \\\ 11 \end{bmatrix}$$
得到
$$
3C + 6D = 5 \\
6C + 14D = 11
$$
同时根据偏导求极值有:
$$\Vert e \Vert^2 = e_1^2 + e_2^2 + e_3^2 \\\ =(C+D-1)^2 + (C+2D-2)^2 + (C+3D-2)^2 \\\ =3C^2 + 12CD-10C+14D^2 -22D + 9 \\
\begin{cases}
\frac{\delta f}{\delta C} = 6C + 12D - 10 = 0 \\
\frac{\delta f}{\delta D} = 12C+28D-22 = 0
\end{cases} \\
即:
\begin{cases}
\frac{\delta f}{\delta C} = 3C + 6D = 5 \\
\frac{\delta f}{\delta D} =6C+14D= 11
\end{cases}
$$
(多项式运算参考:Symbolab)
消元求得,D=1⁄2, C = 2⁄3 所以求得的最佳直线为:y = 2⁄3 + 1/2t
P1 = 7⁄6, P2=5⁄3, P3 = 13⁄6
$$b =\begin{bmatrix}1 &2 &2 \end{bmatrix}$$ e = b - p 于是: e1 = -1⁄6, e2 = 2⁄6, e3 = -1⁄6
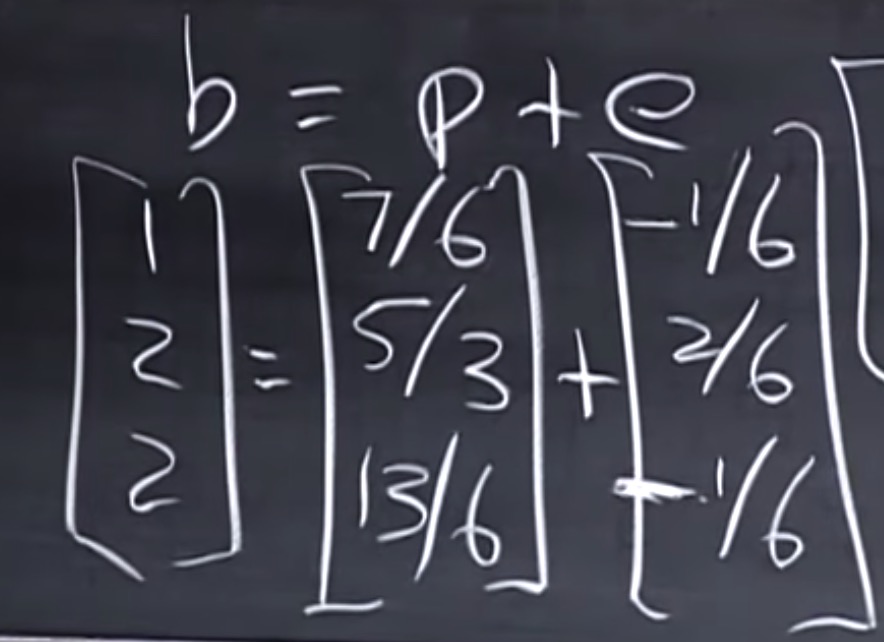
而且有$p \cdot e = 0$ (验证一下)
e同时垂直于列空间的其他向量,比如说(1 1 1 )、(1, 2, 3)垂直(叉积为0)
证明:A的列独立时,$A^TA$可逆
假设$A^TAx = 0$, 那么x=0 (当A可逆,A的零空间只有{0}):
$x^TA^TAx = 0 => (Ax)^T (Ax) = 0 => (Ax)^2 = 0 => Ax = 0$
A有独立列时,且Ax= 0, 那么x = 0
如果列是垂直的单位向量(perpendicular unit vector),那么他们一定是独立的。
垂直的单位向量,又称orthonormal vector - 规划正交向量。



