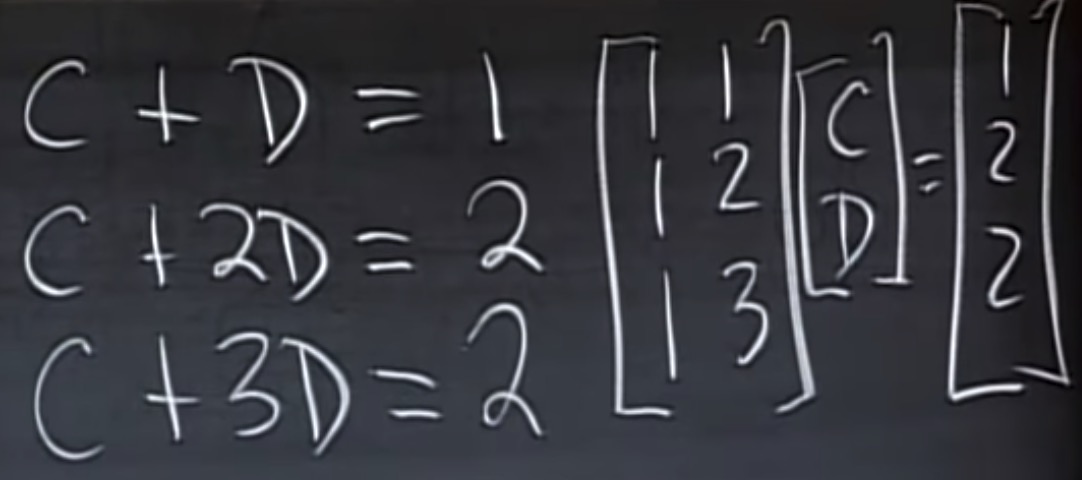MIT 线性代数第15讲:向子空间的投影
Ax=b及最小二乘法
二维情况
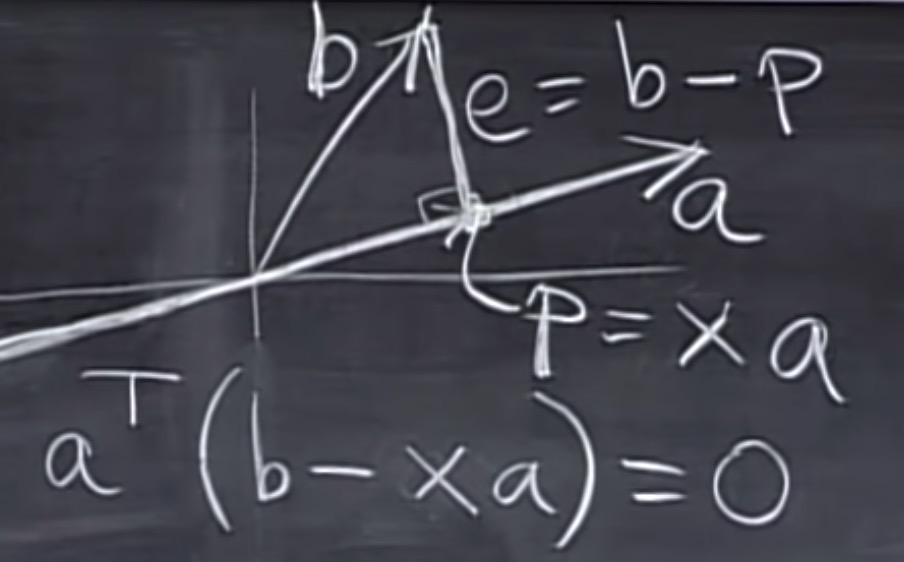
$e \bot a$, 则有
$a^T(b-xa)= 0$
$xa^Ta = a^Tb$
得到: $x = \frac {a^T b} {a^T a}, p = ax => p = a \frac {a^T b} {a^T a} $
$p =({a a^T}/ {a^T a}) b \; p为投影\\\ 或写\;p = Pb \; P为投影矩阵\\\ P = \frac {a a^T} {a^T a} $
解读:
- 假设b’=2b, 长度增加2倍,投影会怎么变化?A:p增加2倍
- 假设a’=2a, 长度增加2倍,投影会怎么变化? A: p 不变化。
- 我们发现,投影是矩阵对向量a的变换。或表示为 投影=[投影矩阵][向量b]
发问:
- P的列空间是什么?
- C(P)是穿过a的直线
- rank (P) = 1
- 对称吗?
- $P^T = P$, 对称
- 对p进行第二次投影会发生什么?
- 第二次投影,p点不动,则有$P^2$=P
引申到多维
- 为什么投影:
- Ax=b也许没有解, 方程数比未知数多。因此把问题转化成b在a上的投影问题。
- 因此解$A \hat x=p$, p是b在列空间上的投影。
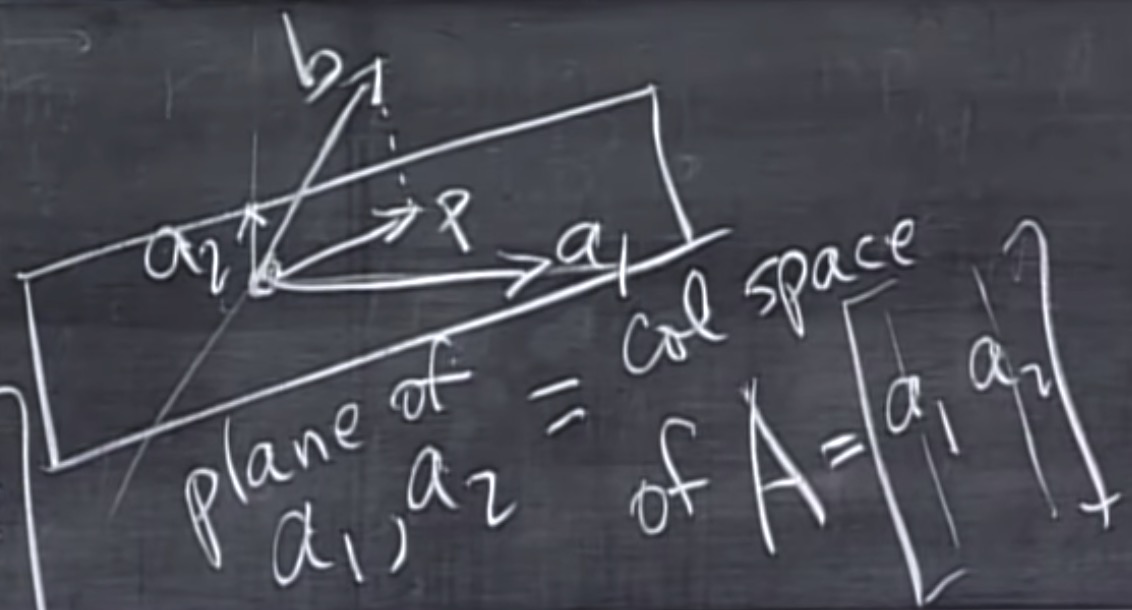
b是不在平面上的一点, b在平面上的投影为p。
a1, a2 是两个独立向量,的平面空间可以定义为以a1, a2为列向量的空间
误差 e = b - p, 垂直于平面
p的形式应该是p=x1a1+x2a2=A$\hat x$
现在的问题专为:$p=A\hat x$, 找到$\hat x$. 已知$e = b-A \hat x$, e 垂直于平面, 即$e \bot a_1, e \bot a_2$ 于是有:
$a_1^T(b-A \hat x) = 0, a_2^T(b-A \hat x) = 0$
写成矩阵形式
$$\begin{bmatrix} a_1^T \\\ a_2^T \end{bmatrix} (b - A \hat x) = \begin{bmatrix} 0 \\\ 0 \end{bmatrix} $$
或写成:
$A^T(b-A \hat x) = 0$
可知e位于$A^T$的零空间,且有$e \bot C(A)$
得到 $A^TA \hat x = A^T b $
$\hat x = (A^TA)^{-1}A^Tb$
投影$p = A \hat x = A(A^TA)^{-1}A^Tb$
投影矩阵:
$$\bbox [5px,border:2px solid red] {P = A \hat x = A(A^TA)^{-1}A^T}$$
解读:
如果进一步演算
$$ P = A(A^{T}A)^{-1}A^T = A A^{-1} (A^T)^{-1} A^T = I $$
我们得到了单位矩阵,问题出在哪?
A:
- A不是方阵,因此没有逆矩阵,所以不能进一步拆解
- 如果A是方阵且可逆,那么他的列空间是整个$R^n$。 如果我投影到$R^n$的投影矩阵矩阵是什么?是单位矩阵(因为这个投影什么都不需要做,对原来的向量不需要做任何改变。如果将b投影到$R^3$, b本身位于列空间,所以这个投影是单位矩阵。)
- 回忆1维的例子,$P = \frac {a a^T} {a^T a} $. 有点像
- 我们和别的投影矩阵一样,我们对这个投影矩阵有什么样的期待?
- 对称, $P^T = T$
- $P^2 = P$? 证明: $$ P^2 = A(A^T A)^{-1} A^T A(A^T A)^{-1} A^T \\\ = A(A^T A)^{-1}\;(A^T A(A^T A)^{-1}) A^T \\\= A(A^T A)^{-1} A^T $$
总结:
如果b位于列空间, Pb=b, (想像桌面上的铅笔的投影没有变化) $$ P = A(A^T A)^{-1} A^T \\
b = Ax \\
Pb = A(A^T A)^{-1} A^T Ax \\\= A((A^T A)^{-1} A^T A)x \\\ = Ax \\\= b $$如果b垂直于列空间,Pb=0, (想象铅笔垂直于桌面)
什么向量垂直于列空间?答案是$N(A^T)$的向量, $A^T$的零空间的向量。
例题:
问题:
解答: