向量正交和子空间正交

子空间：

• 子空间的维数，和垂直

向量正交

• $x \bot y$, 则有$x^Ty=0$。证明：

  • 如果$x \bot y$, $\Vert x \Vert^2 + \Vert y \Vert ^2 = \Vert x + y \Vert^2$
    • 长度的平方：$\Vert x \Vert^2 = X^TX$
    • $\Vert x \Vert^2 + \Vert y \Vert ^2 = \Vert x + y \Vert ^2 = x^Tx + y^Ty = (x+y)^T(x+y) = x^T x + y^T y + x^Ty + y^Tx$
    • => $0 = x^Ty + y^Tx = 2x^Ty$
    • => $x^Ty=0$

• 零向量与任何向量正交

• 子空间正交

  • S与T正交，S空间的所有向量与T空间的所有向量正交
    • 墙与地面不正交
    • 两个墙面的交线与地面正交
  • 交点为零向量
  • 平面的子空间包括
    • 通过零向量的直线垂直平面：永不
    • 通过零向量的直线垂直零向量：永远
    • 通过零向量的直线垂直另一个通过零向量的直线：两条线垂直90度，只相交于原点
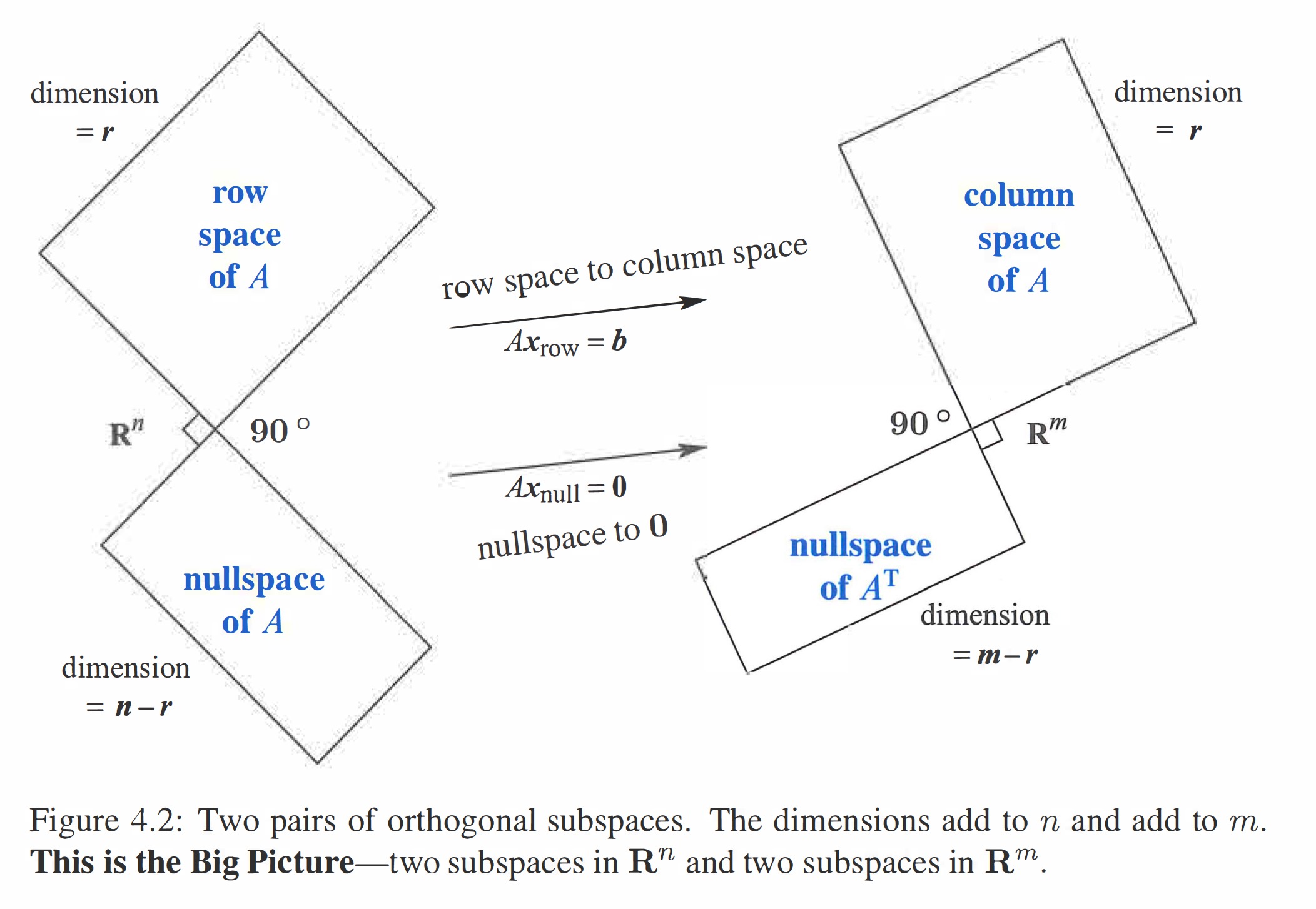
  • 行空间与零空间正交：证明
    • 行空间有Ax = 0，$\begin{bmatrix} 矩阵A的第1行\\\ 矩阵A的第2行\\\\ 矩阵A的第n行\end{bmatrix}\begin{bmatrix} X \end{bmatrix} = \begin{bmatrix} 0 \\
      0\\\\ 0 \end{bmatrix}$
    • X与A的每一行垂直
    • A每一行的线性组合和X垂直
  • $C(A)\bot N(A^T)$
  • 例子： $A=\begin{bmatrix} 1& 2 & 5 \end{bmatrix} \begin{bmatrix}x_1 \\\ x_2 \\\ x_3 \end{bmatrix} = \begin{bmatrix}0 \end{bmatrix}$
    • n = 3?
    • dim N(A) = 2
  • 零空间和行在$R^n$空间内正交互补。零空间包含的所有向量垂直于行空间。

• 解Ax=b，m > n, 无解的时候， 找到最接近的解

  • $A^TA$
    • 行列数相等
    • 对称：证明：$(A^TA)^T = A^TA$
    • 可逆吗？
    • 由$A^TA$得到$A^TA \hat x = A^Tb$, $A^TA$可逆吗？
      • A有独立列时，$A^TA$可逆