Linear Albegra Lecture 1 - Geometry of Linear Equations
Linear Equations vs line and pland vs vectors.
Linear equations:
$$2x - y = 0 \\
-x + 2y = 3$$
Write in matrix, we have:
-x + 2y = 3$$
$$
\begin{bmatrix}
2 & -1 \\
-1 & 2y \end{bmatrix} \begin{bmatrix} x \\
y \end{bmatrix} = \begin{bmatrix} 0 \\
3 \end{bmatrix} $$
or in short $$ A X = b $$
A is called the matrix, X is the unknown.
-1 & 2y \end{bmatrix} \begin{bmatrix} x \\
y \end{bmatrix} = \begin{bmatrix} 0 \\
3 \end{bmatrix} $$
The tow picture:
row is presents a line and the joint point of line is the solution of the linear equations.

$$
x
\begin{bmatrix}
2 \\
-1 \end{bmatrix} + y \begin{bmatrix} -1 \\
-2 \end{bmatrix} = \begin{bmatrix} 0 \\
3 \end{bmatrix} $$
This is linear combination of columns, which represents adding two vectors and get the result of third vector.
-1 \end{bmatrix} + y \begin{bmatrix} -1 \\
-2 \end{bmatrix} = \begin{bmatrix} 0 \\
3 \end{bmatrix} $$
Column picture:
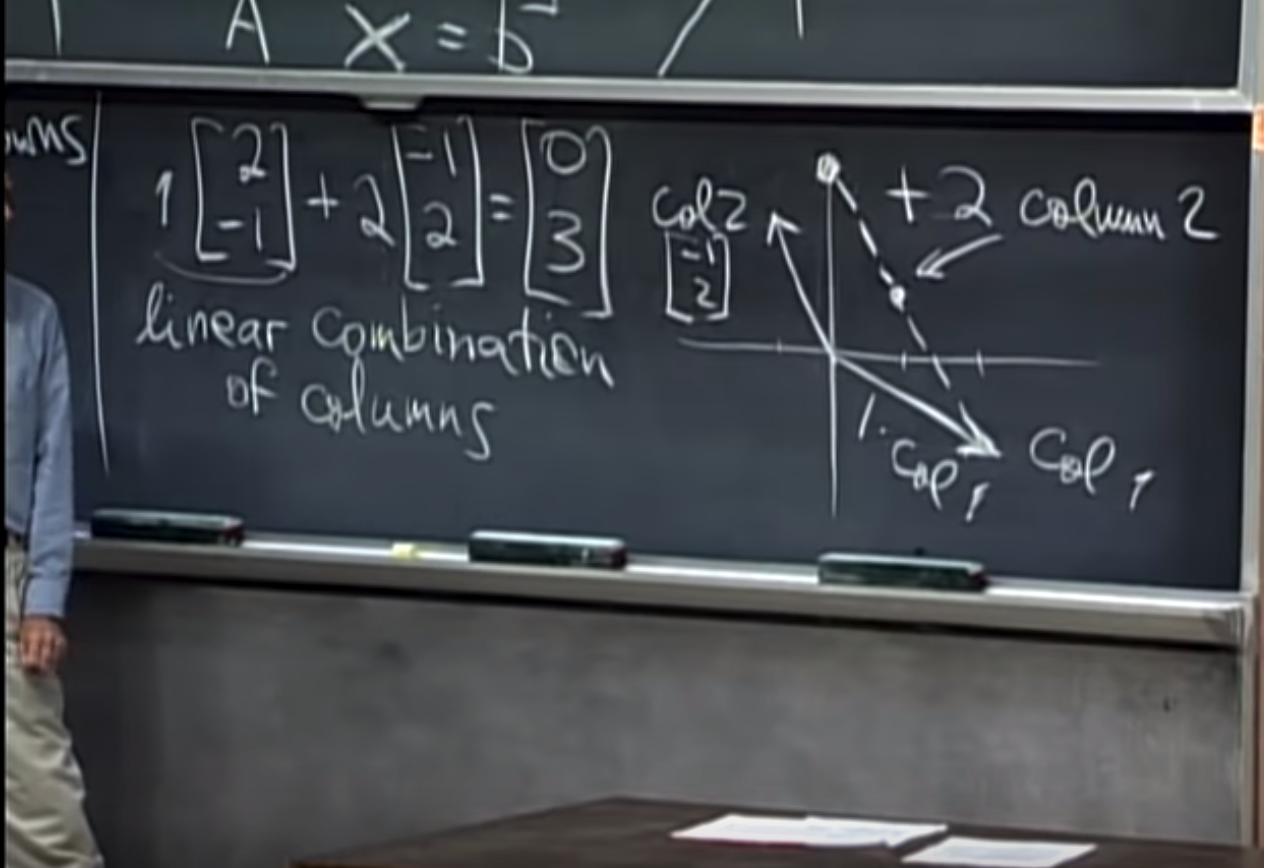
In 3D, row picture represents a plane.

3D column picture is three vectors added up to be the fourth vector b.
Think about the cases we do no have a solutions.
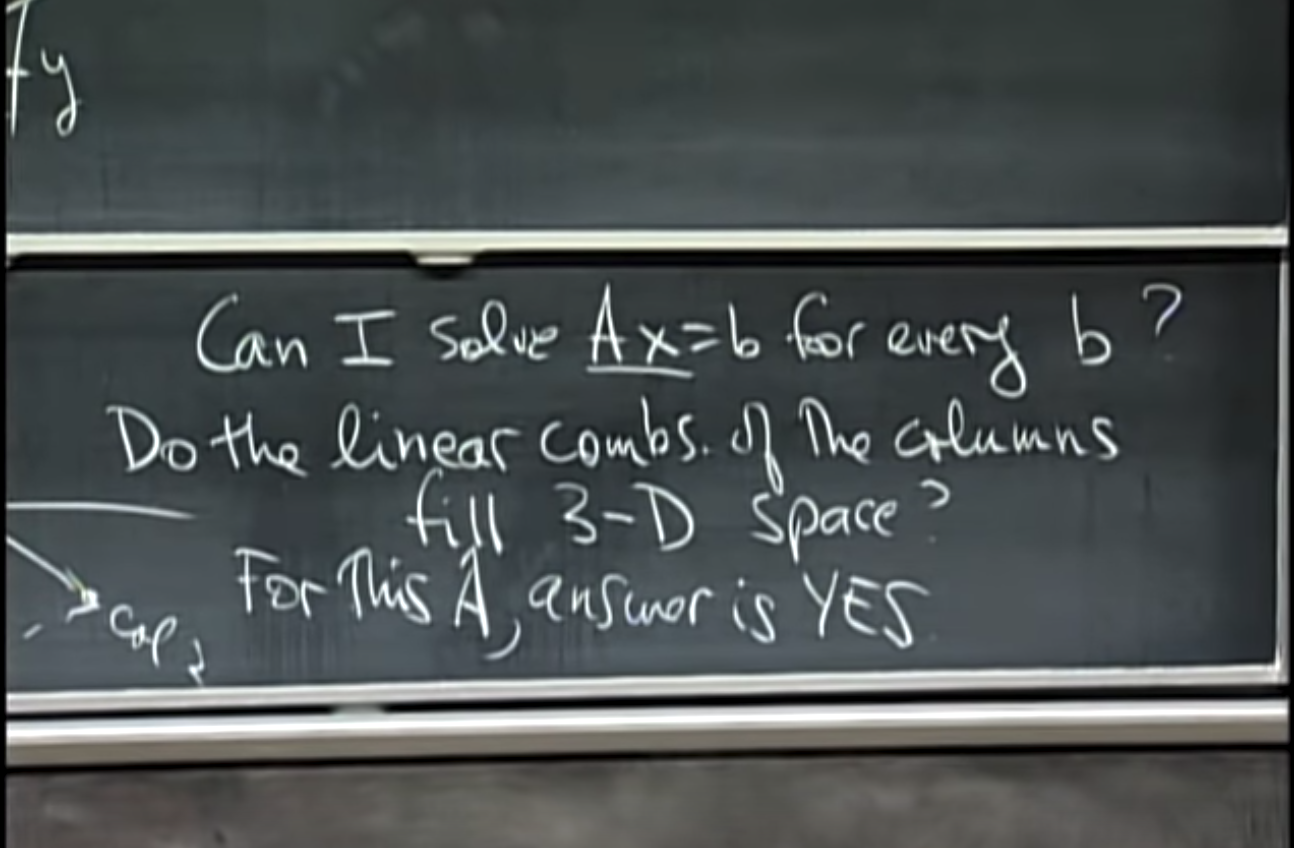
link to original lecture: https://ocw.mit.edu/courses/mathematics/18-06-linear-algebra-spring-2010/video-lectures/lecture-1-the-geometry-of-linear-equations/

