如题.

假设矩阵A行列数是mxn， m < n（未知数多于等式数），于是存在有Ax=0的非零解。此矩阵至少有一个自由变量。

Independent: 线性独立：或称为线性无关。系数非0的线性组合不为0.

​ 向量互相独立，则他们构成的矩阵的零空间是零向量。

​ 例子1：

​ 两个向量，v1, v2=2v1, 有-2v1+v2=0, 结论：线性不独立。

​ 例子2：

​ v2=0, v1$\ne$0, 0v1+1v2 =0, 线性不独立：如果含有0向量，则此组向量不独立

​ 例子3：

​ v1, v2, v3 $\ne$ 0. 如果m<n（行数少于列数），对于下述矩阵，存在零空间，给出v1, v2, v3的线性组合为0.

结论：

**如果向量独立，则C(A)={0}、rank=n, 没有自由变量. **

如果不独立则Ac=0，则在零空间内存在不为{0}的c、rank<n，存在自由变量

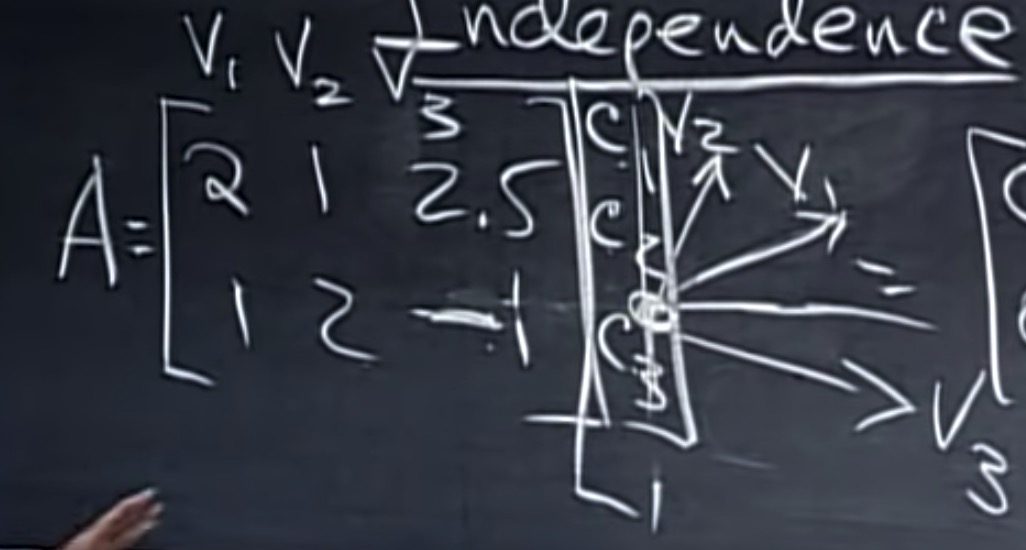
线性非独立， 则存在C，C非零，而且Ac=0成立。

pivot column：枢轴列

span the space: 线性生成空间 wiki, 所以可能的组合； 空间是所有向量的线性组合。

rank of A: A的秩=枢轴列的个数=列空间的维度（subspace)

一个有实际意义的问题是找出一组向量，能长成一个所需要的空间， 但是这里头不存在没用的自由向量。引出基的概念

basis： 基 ：1 组合线性独立向量 2 并生成线性空间

例子：$R^3$的一个基, 如下图， 根据定义验证

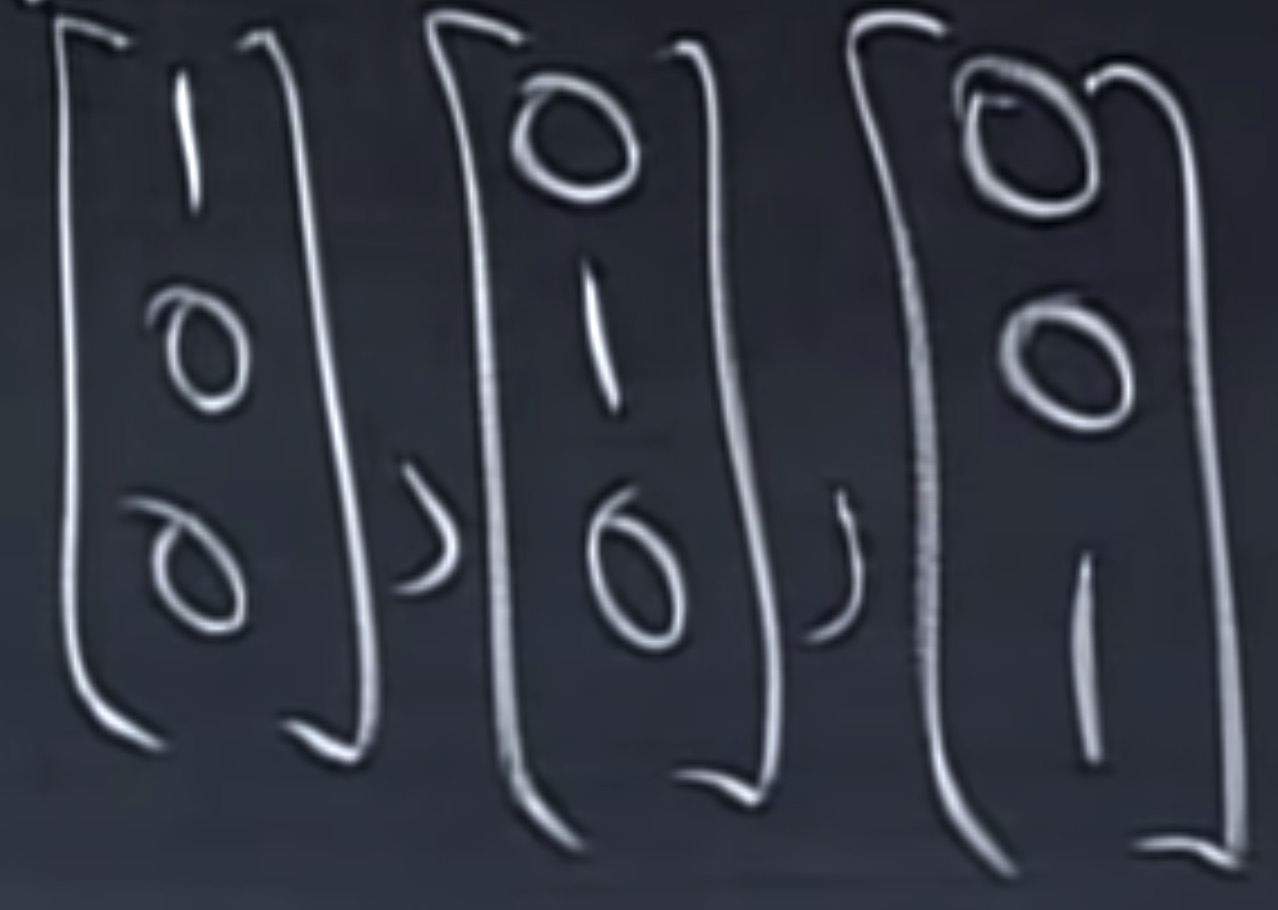
例子2：下例线性独立， 但是不能长成$R^3$,那么添加一个什么样的向量会张成$R^3$?

总结：n个向量成为基的条件是所构成的nxn矩阵可逆。

但上面的例子可以构成三维中2维平面的基。

由上面的例子引出：

所有构成空间的基的向量的个数，都和此空间的维数相等。

下例：张成空间吗？是的。 是空间的基吗？不是。

它的基是啥？第1，2列。rank=2。

结论：rank=主元个数=列空间C(A)维数

1，3也可以构成基。

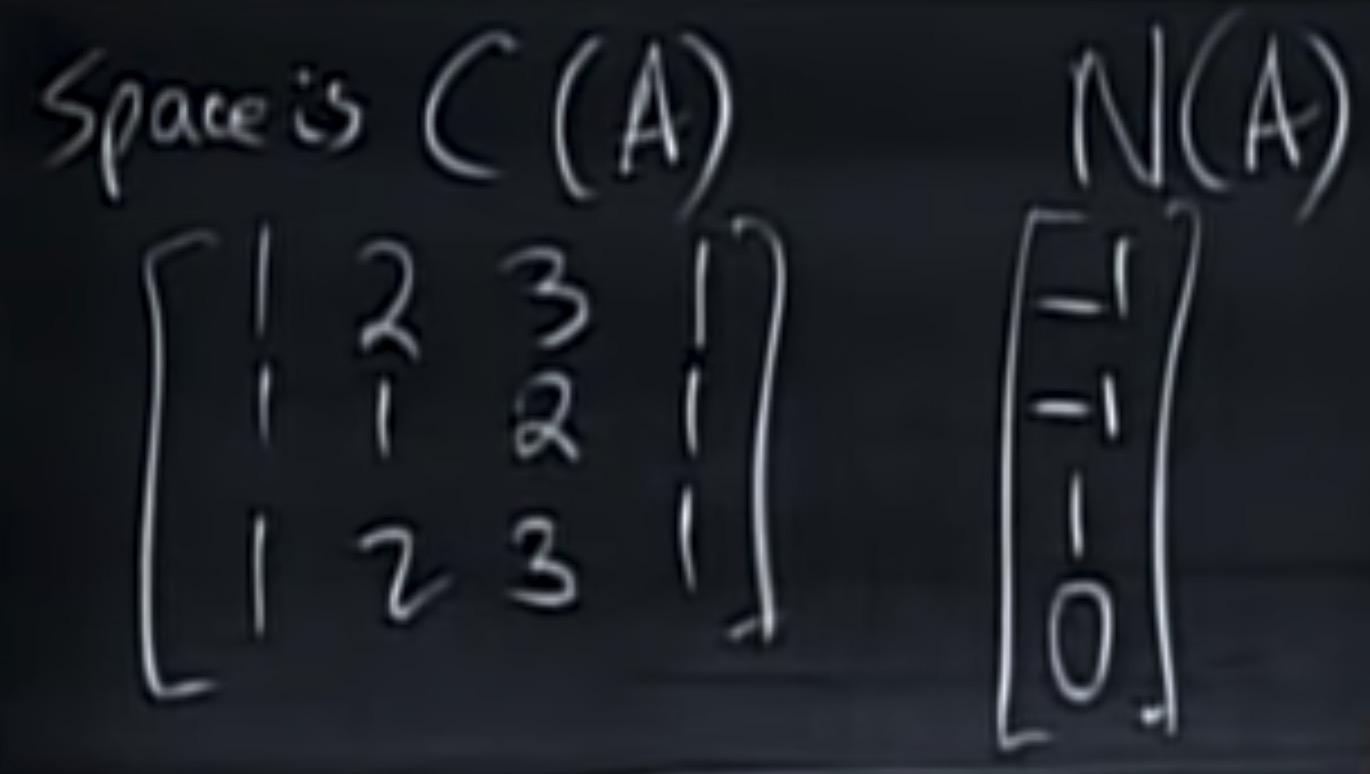
null space: 零空间的维数=自由变量的个数=空间的维数-矩阵的秩

上面的例子，又可以给出另外一个0空间的向量。

问题：他们是空间的基吗？他们独立吗？引出零空间的维度。

结论：零空间的维度是自由变量的个数。dim N(A)=自由变量的个数=n-rank

invertable： 不可逆。 说明rank(A) < n

任何一个空间的基都有相同数量的向量，且与空间的维度相等。

参考： youtube