线性代数讲座 11: 矩阵空间
新向量空间的基础,秩为1的矩阵,小世界图画

例子:下面的矩阵,能构成空间基吗?
它的行不独立,使得列不独立,此矩阵不可逆,因为有两行相等,
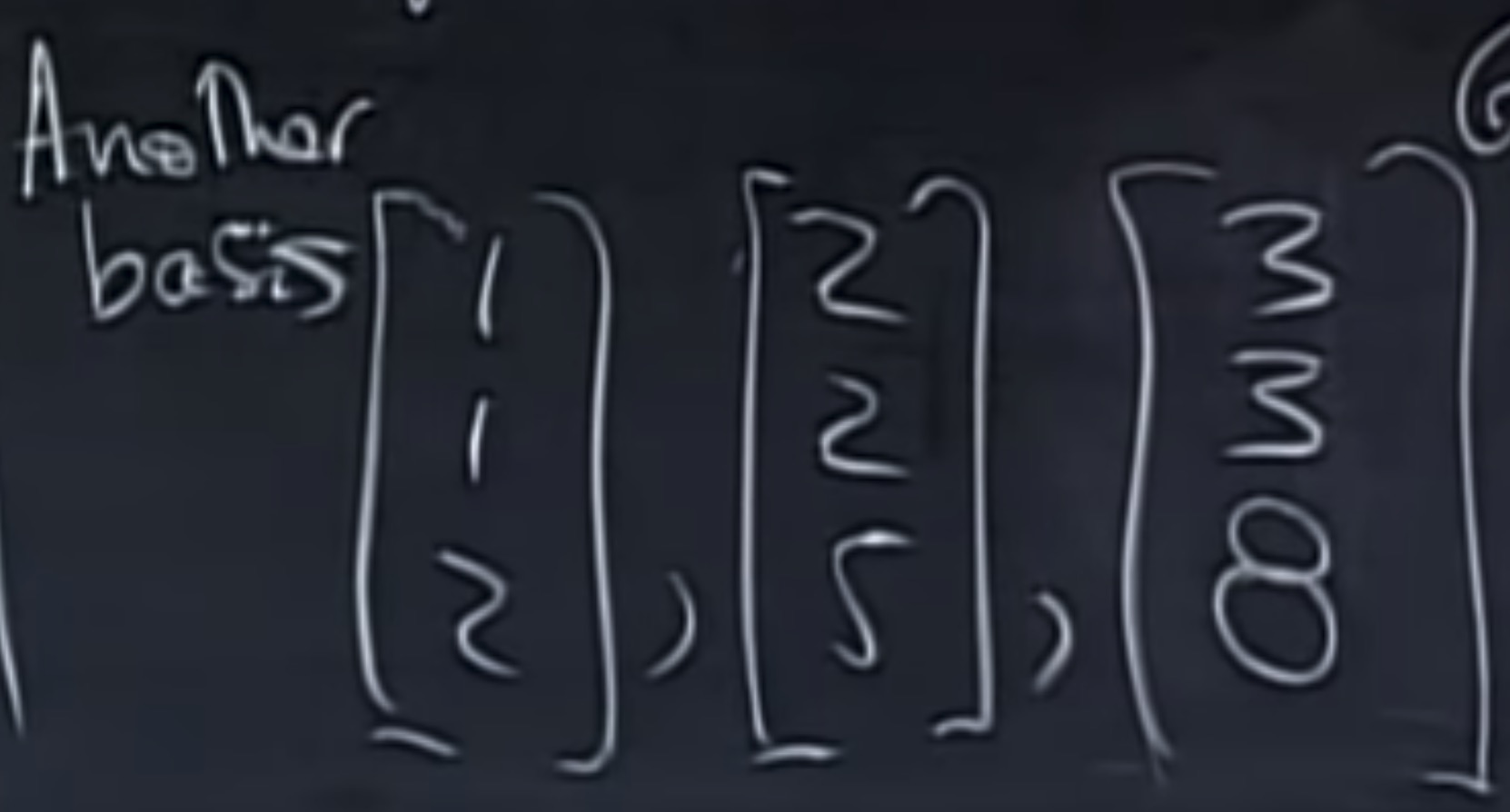
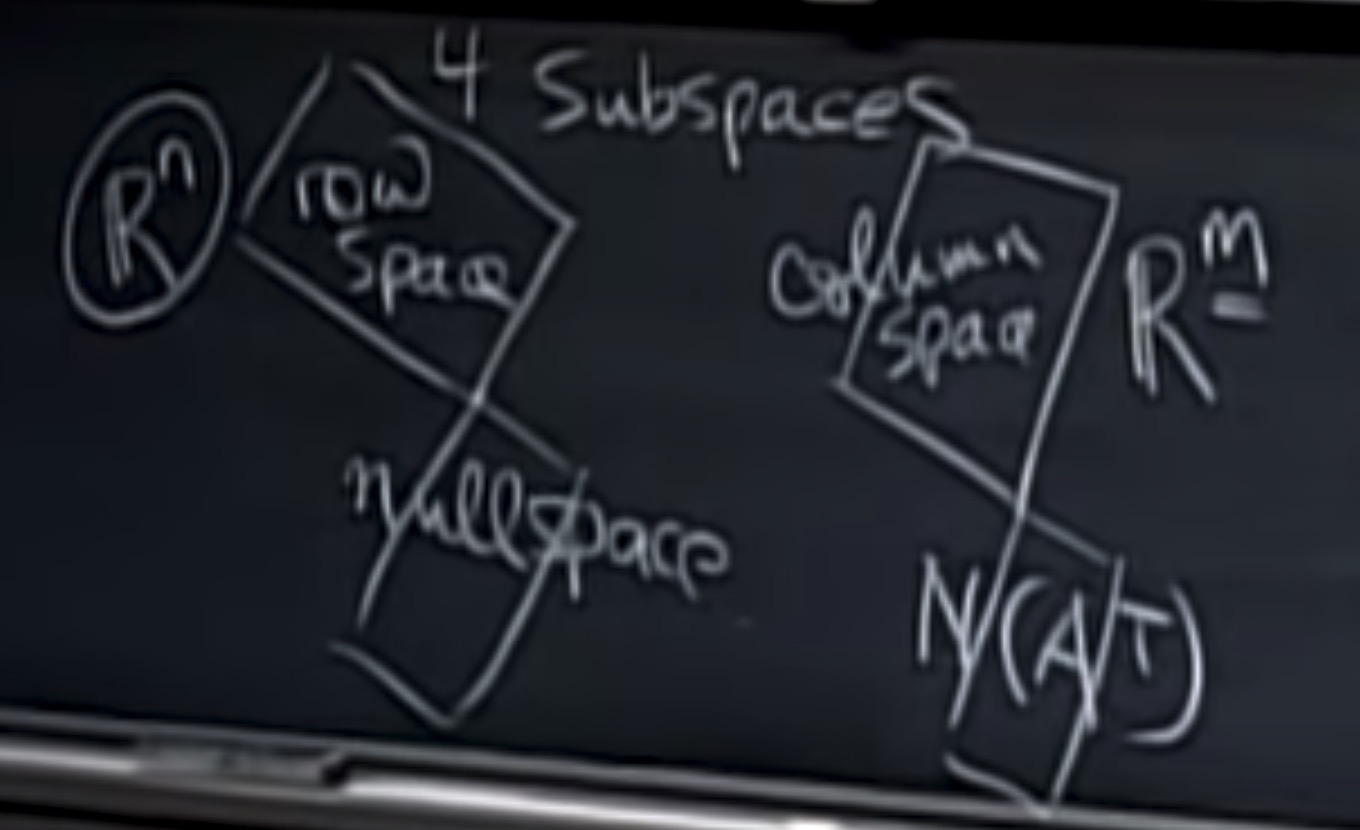
列空间:C(A) 位于$R^m$, m = 行数, dim A = r, 基为主元列
零空间 N(A), 位于$R^n$. dim N(A) = m-r
引出行空间:=$C(A^T)$, 位于$R^n$, n = 列数, 位于$R^n$, dim $A^T$ = r = dim A
行空间的零空间=$N(A^T)=$左零空间, 位于$R^m$, dim $N(A^T)$ , dim N(A) = n -r
例子:做消元后,C® <> C(A),
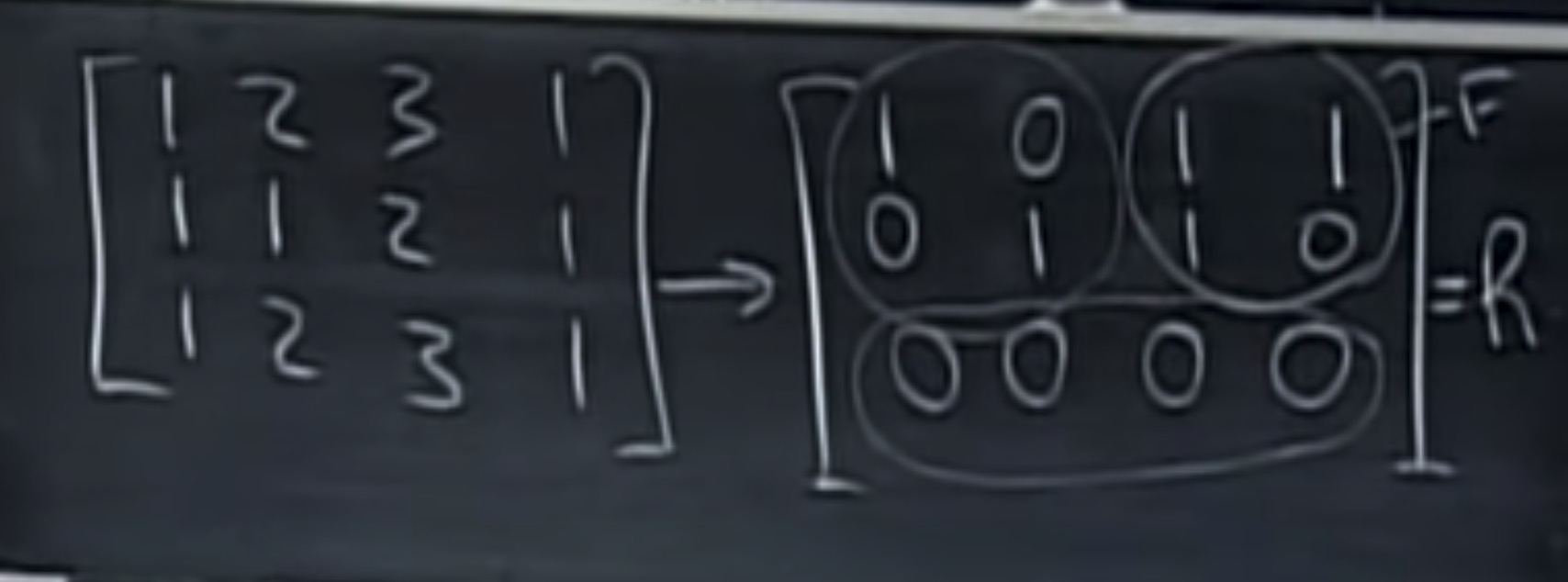
问题:消元后改变行空间吗???不改变,因为消元的过程对行来讲是线性组合的过程。
上例消元后,基为R的头r行
左零矩阵的来历: $$ A^Ty=0, 对两边转置,得到y^TA=0^T $$ 计算左零空间的基:
高斯-约旦消元的过程,将[A I]变成[R E]. 或者说EA=R, 现在是求出E,R=I,所以E=$A^{-1}$
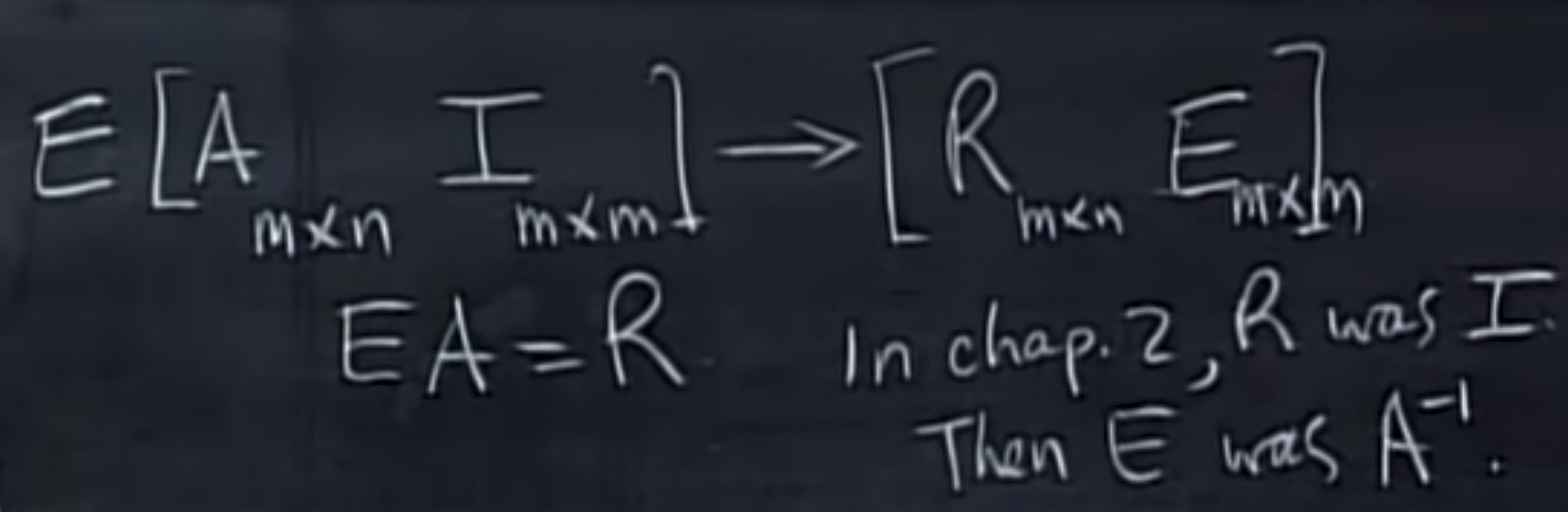
画一个单位矩阵,重复上面的消元过程,得到:
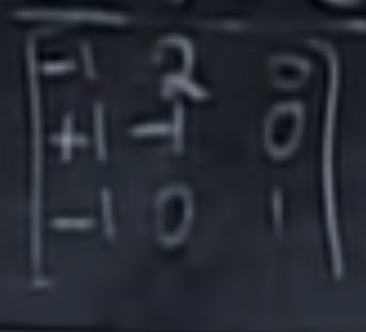
于是EA可以写成:

左零空间的维数是1,所以有左零空间的向量个数是1,它是(-1 0 1).
另一个解读:列零空间有列的组合变成0, 行空间是行的组合变成零。上面的例子,为是行组合变成0, 显然有(-1 0 -1),构成最下面的一行零。
矩阵空间
我们可以想象一个空间, 它由矩阵组成, 而不是之前说的向量. 只要满足线性空间的封闭性原则即可.
将所有的 3×33×3 矩阵看做了一个线性空间,那么它的子空间有:
- 上三角矩阵
- 对称矩阵
- 对角矩阵。
仔细观察可以发现, 上三角矩阵与对称矩阵的交集为对角矩阵
初步了解一下矩阵空间的基, 看下面例子:
$$
\begin{bmatrix}
1 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & 3 & 0 \\
0 & 0 & 0
\end{bmatrix}
\begin{bmatrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 7
\end{bmatrix}
$$
可以发现,任何三阶对角矩阵均可用这三个矩阵的线性组合生成,因此,他们生成了三阶对角矩阵空间,即这三个矩阵是三阶对角矩阵空间的一组基。
也可以换个角度看待矩阵空间的问题, 我们可以将矩阵看成若干列, 然后将这些列再组成一个长长的列, 那么这个列就等效于之前那个矩阵了. 然后我们就可以使用之前学过的向量空间的概念来理解矩阵空间了. 其实很多算法也是这么实现的.
基与维数
假设一个 3×3 矩阵,其矩阵空间 M
则 M 的一组基为:
$$
\begin{bmatrix}
\boldsymbol 1 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0
\end{bmatrix}
\begin{bmatrix}
0 & \boldsymbol 1 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0
\end{bmatrix}
\begin{bmatrix}
0 & 0 & \boldsymbol 1 \\
0 & 0 & 0 \\
0 & 0 & 0
\end{bmatrix}
\\
\begin{bmatrix}
0 & 0 & 0 \\
\boldsymbol 1 & 0 & 0 \\
0 & 0 & 0
\end{bmatrix}
\begin{bmatrix}
0 & 0 & 0 \\
0 & \boldsymbol 1 & 0 \\
0 & 0 & 0
\end{bmatrix}
\begin{bmatrix}
0 & 0 & 0 \\
0 & 0 & \boldsymbol 1 \\
0 & 0 & 0
\end{bmatrix}
\\
\begin{bmatrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
\boldsymbol 1 & 0 & 0
\end{bmatrix}
\begin{bmatrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & \boldsymbol 1 & 0
\end{bmatrix}
\begin{bmatrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & \boldsymbol 1
\end{bmatrix}
$$
很容易知道, 维数就是 9 (九个基)
仔细看看就知道, 三阶对称矩阵空间有 dim(S)=6(因为知道上或下三角的三个6个数就知道其他数了) 、上三角矩阵空间有 dim(U)=6(和对称矩阵一个道理)、对角矩阵空间有 dim(D)=3 上三角矩阵与对称矩阵的交集为对角矩阵, 即 S∩U=D, 而且其秩为 3.
那么并集呢? 回忆之前的介绍, 并集不能构成子集, 不过我们可以考虑另一个情况, 两个空间的和: S+U:
将 S 与 U 进行线性组合, 这个集合就是 M, 秩为 9.
通过将U和S进行组合,我们还可以得到其他子空间,比如前面已经提过的对称阵空间S和上三角阵空间U的交集 得到的对角阵空间D,其维数是3维。
但是注意并集 组成的集合不是子空间,要将符号改成“+”,即S+U才构成子空间,如果每次任取S内任一元素加上U内任一元素,我们可以得到所有3*3矩阵,因此这个S+U构成的空间维度是9,这里我们可以发现dim(S)+dim(U)=dim(S交U)+dim(S+U),即S的维度加上U的维度等于它们交的维度加上它们和的维度,以上就是关于矩阵空间的内容,除了向量跟传统的向量有区别,其他都是一样的求法。
现在我们再举个比较特殊的例子,假设有一个矩阵空间,它来自于微分方程,该微分方程为d2y/dx2+y=0,其解是y=cos( x) ,y=sin( x),这个微分方程的零空间或解空间就是这两个解的线性组合,也就是y=c1cos(x)+c2sin(x),很铭明显这个向量空间的维数是2,因为它有2个基:cos(x)和sin(x)。举这个例子的目的在于:cos(x)和sin(x)看起来并不像向量,有些像函数,但我们可以称它们为向量,因为其可以做数乘也可以作加法,所以可对它们进行线性组合,这就是线性代数中的向量,基,维数,它们不仅仅局限于我们平常所熟悉的向量形式,也可以用于矩阵甚至函数等,只要它们满足向量的特性。
秩一矩阵
对于矩阵:
$$
A =
\begin{bmatrix}
1 & 4 & 5 \\
2 & 8 & 10
\end{bmatrix}
=
\begin{bmatrix}
1 \\
2
\end{bmatrix}
\begin{bmatrix}
1 & 4 & 5
\end{bmatrix}
$$
行空间和列空间的维数都为 1,秩一矩阵都可以写为: $A=uv^T$,这里的U 和 V 都是列向量.
可以将秩一矩阵看成是”积木”, 用它可以搭建任何矩阵
秩一矩阵类似“积木”,可以搭建任何矩阵,如对于一个 5×17 秩为 4 的矩阵,只需要 4 个秩一矩阵就可以组合出来.
举一个例子,在 R4 中, 假设 $ v = \begin{bmatrix} v_1\\\ v_2 \\\ v_3\\\ v_4 \end{bmatrix} $ , S是满足条件 v1+v2+v3+v4=0 的所有向量组成的空间.
为什么 SS 是一个空间呢? 因为 v1+v2+v3+v4=0 这个特点说明它对加法和数乘封闭, 而且 SS 包含零.
v是A=[1 1 1 1]的零空间。
r(A)= 1
它的维度是多少? 3, 因为v1, v2, v3独立,而v4不独立。
它的rank=1, 所以dim N(A) = n-r = 4-1 = 3
$$
dim \;N(A^T) = 1 \\\
零空间的基:检查3个自由变量。有3个, 如下图\\
dim C(A) = 1, C(A)=R^1, N(A^T) = {0}, dim\;N(A^T) = 0
$$
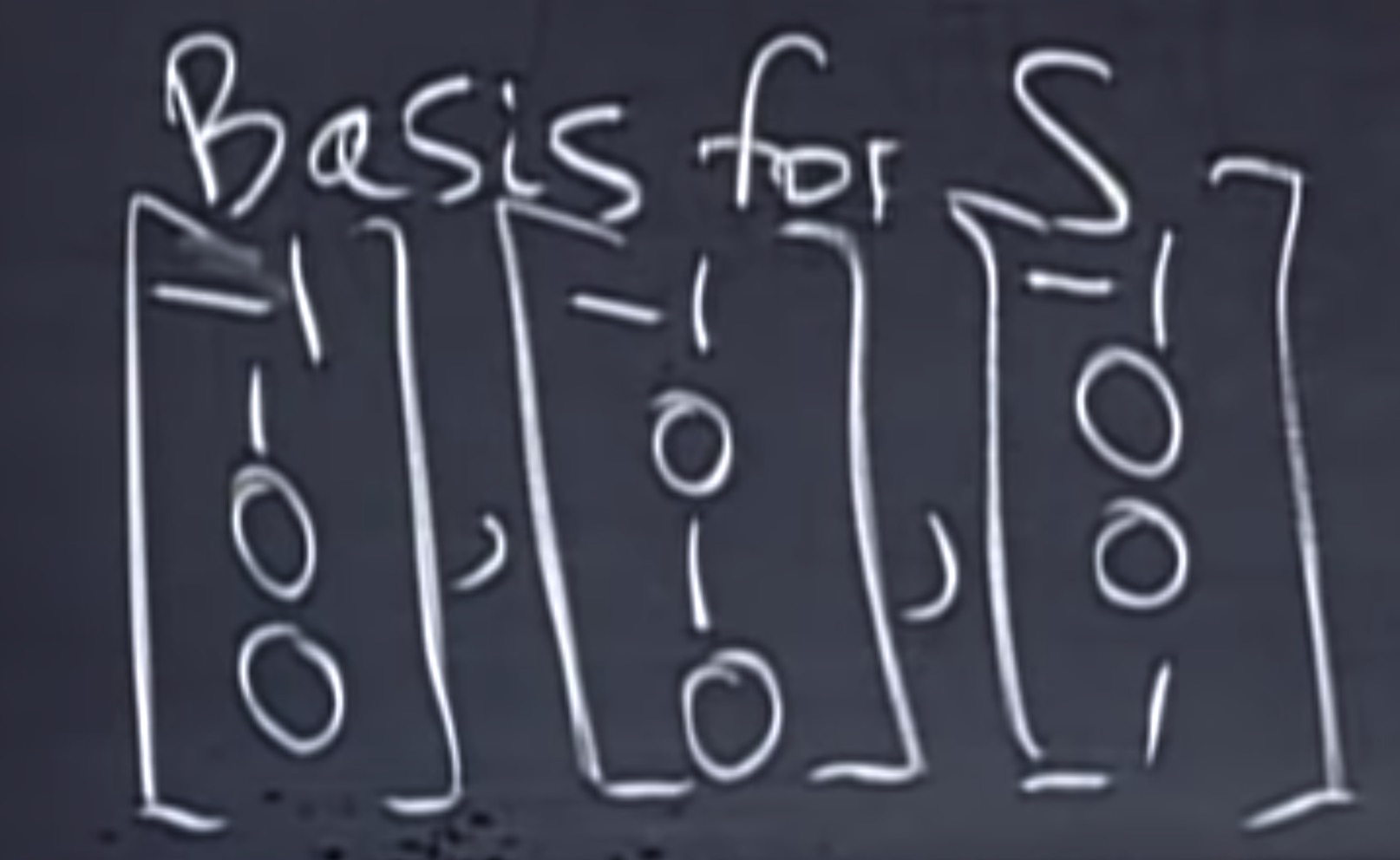
从上面秩一矩阵的方法来看,v1+v2+v3+v4=0v1+v2+v3+v4=0 等价于: $$ \begin{bmatrix} 1 & 1 & 1 & 1 \end{bmatrix} \begin{bmatrix} v_1\\\ v_2 \\\ v_3\\\ v_4 \end{bmatrix} = 0 $$ S就成为了 A= $ \begin{bmatrix} 1 & 1 & 1 & 1 \end{bmatrix} $ 的零空间。 rank(A)=1 ,它的零空间的维数就是 n−r=3

