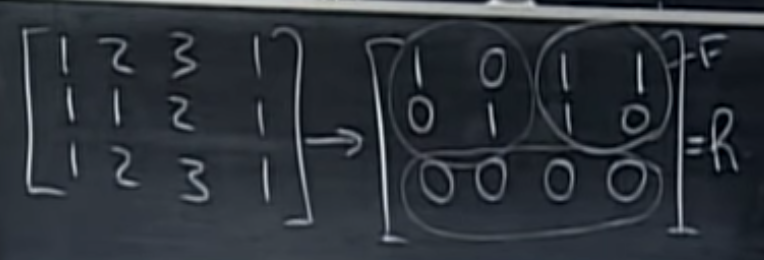四个基本的子空间和$R^n到R^{n \times n}$的扩展

例子 1：最简单的$R^3$空间：$R^3$的标准基空间（standard basis）

$$ \begin{bmatrix} 1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \end{bmatrix} $$

例子2：有三个向量的基空间

$$ \begin{bmatrix} 1 \\
1 \\
2 \end{bmatrix} , \begin{bmatrix} 2 \\
2 \\
5 \end{bmatrix} , \begin{bmatrix} 3 \\
3 \\
8 \end{bmatrix} $$ 解说： 此三个向量构成的矩阵，不构成基空间，因为第一行和第二行相同，此三个向量构成的矩阵不可逆。此构成矩阵的行不独立，所以此三个列不独立。

子空间：

  • 列空间C(A)
  • 零空间N(A)
  • 行空间: 所有行的线性组合 = 所有$A^T$矩阵列的线性组合 = $C(A^T)$
  • $A^T$的零空间=$N(A^T)$=左零空间(Left nullspace)

设有$A_(m \times n)$:

  • 列空间$C(A_{m \times n})$
    • 在$R^m$空间内
    • dim C(A) = rank(A) = r
  • 零空间N(A)
    • 向量有n个元素
    • Ax=0的解
    • 在$R^n$空间内
  • 行空间: 所有行的线性组合 = 所有$A^T$矩阵列的线性组合 = $C(A^T)$
    • 在$R^n$空间内
  • $A^T$的零空间=$N(A^T)$=左零空间(Left nullspace)
    • 在$R^m$空间内

Q: 一个给定的空间，他的基空间是啥？他的维度是多少？

  • 列空间：

    • dim C(A) = rank(A) = r
    • 基：枢轴列(pivot columns)

  • 行空间：

    • dim C($A^T$)= rank(A) = r

    • $$ A = \begin{bmatrix} 1 & 2 & 3 \\
      1 & 2 & 3 \\
      2 & 5 & 8 \end{bmatrix} $$ rank(A) = 2

    • 行空间的基

    列空间改变了吗？

    $C(R) \ne C(A)$ （\[ 1 1 1\] 在C(A)中，不 在C®中)

    A或R的基是R的头两行

  • 零空间

    • 空间基是矩阵的特殊解，等于自由变量的个数=n-r
    • r = 枢轴变量的个数，n-r自由变量的个数

  • 行向量的零空间

    • dim $A^T$ = m - r
    • 基空间
    • $A^Ty=0 => y^TA^{TT} = 0^T => y^TA=0T$ 左零空间

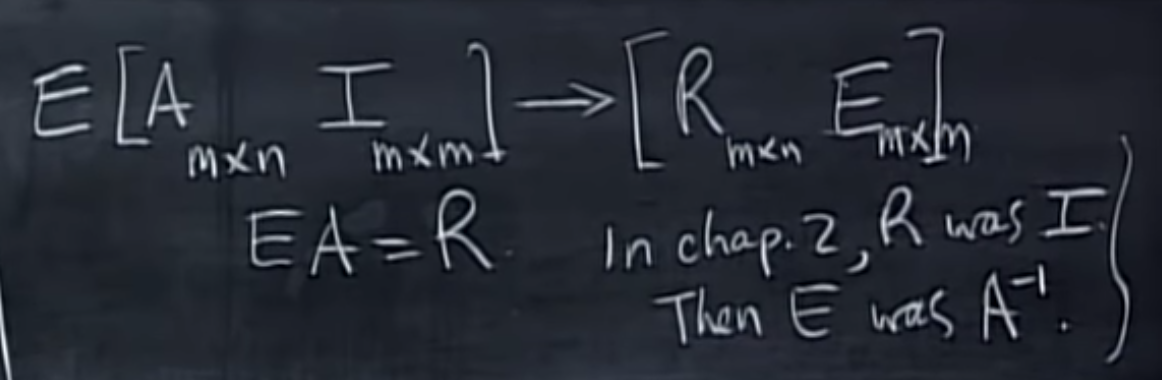
矩阵空间 M : $R^n到R^{n \times n}$的扩展

所以对向量的线性操作都适用于矩阵

可以把矩阵当成向量，构成新的空间

  • M的子空间，或者对于所有3X3矩阵
    • 上三角矩阵
    • 对称矩阵
    • 对角矩阵D：上两个矩阵空间的交集，
    • 下图构成$R^{3 \times 3}$空间，并且是此空间的基矩阵：
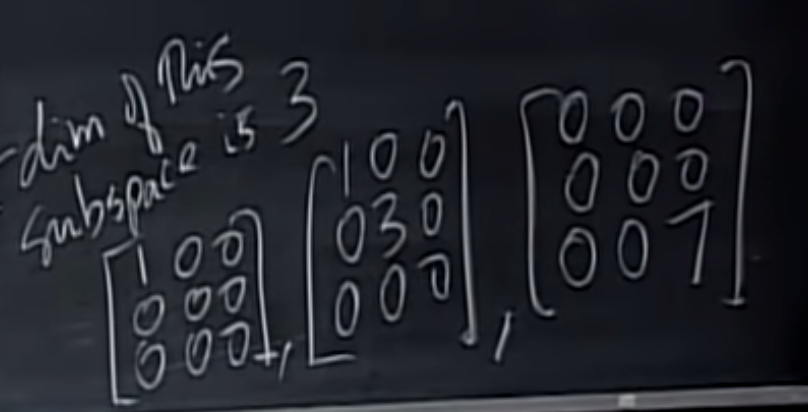
    • 上述矩阵独立
    • 上述矩阵生成$R^{3 \times 3}$