直线法线式方程的几何证明

直线法线式方程百度百科上的公式推导过于繁琐，不够直观。 这里给出法线式 x * cosθ + y * sinθ - d = 0 的几何证明。并推广到n维超平面。

几何证明：

在直角坐标系画任意斜线l，从坐标原点O画垂直于l的线段m,垂足为S。 取l上任一点P(x, y)。从坐标(x, 0)引垂直于m的线段n，垂足为Q。从P(x, y)引垂直于n的线段PR，垂足为R。

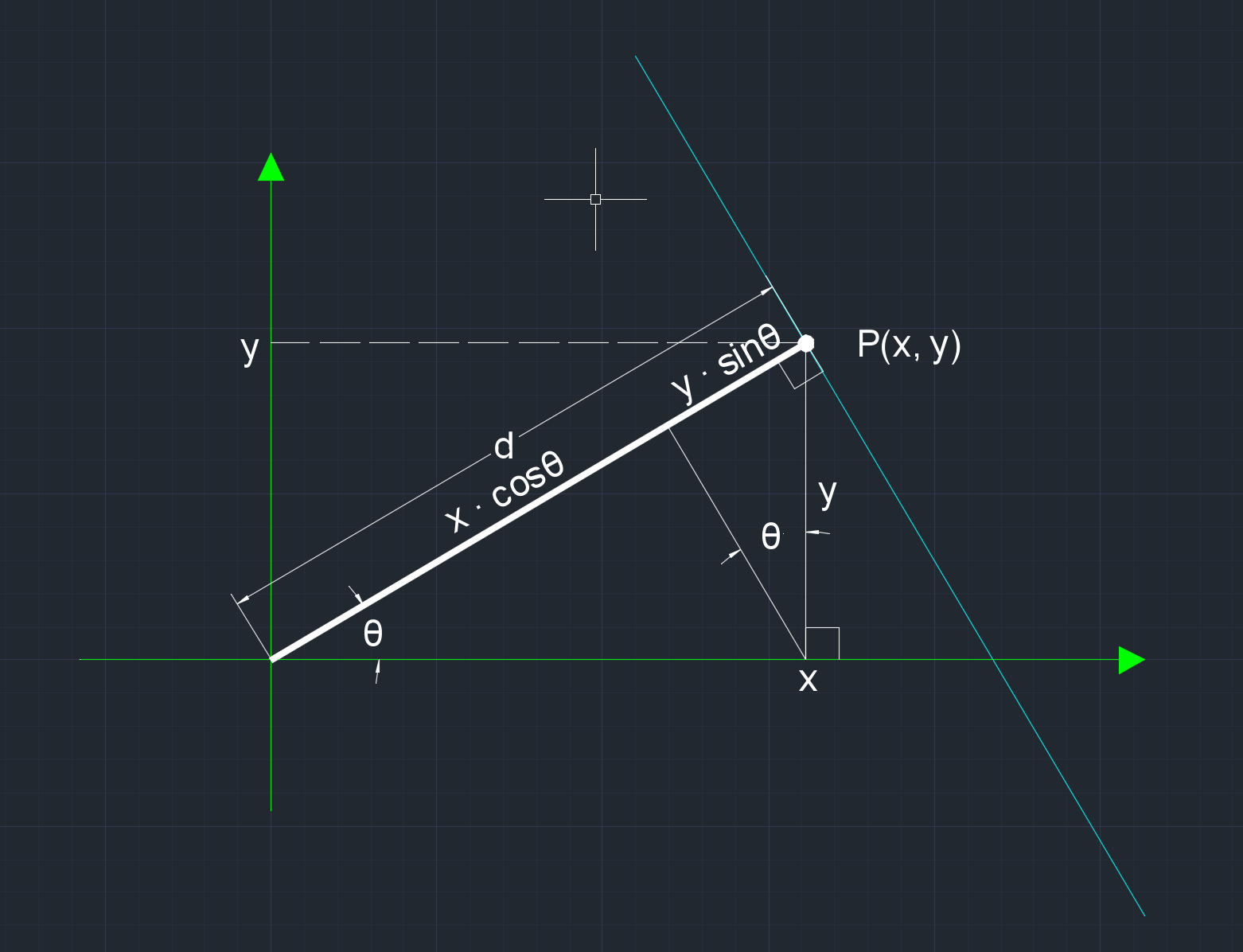
原点O到直线l的距离

​ d = OQ + QS

OQ = x * cos θ， QS = y * sin θ

则 x * cos θ + y * sin θ - d = 0

推广：

设线段OS与X轴的夹角为 $$ω_x = θ$$ 线段OS与Y轴的夹角为 $$ω_y = 90°- θ$$

则得$$ x * cos(ω_x) + y * cos(ω_y) - d = 0$$

写成行列式：

​

三维平面的法线式则有：

​

更高维超平面可以简写为

​ $$\vec{ω} ·\vec{X} - d = 0$$

可以描述成：

1. 超平面上各点到原点的连线，在与超平面平行方向的投影长度，等于超平面法线的长度。

2. 超平面法线的长度，等于每个轴的坐标在超平面法线方向的投影到坐标原点的距离之和。

利用勾股定理证明：

三维情况下空间任一点到原点的距离为

$$d = \sqrt{x^2 + y^2+z^2}$$

得到$$x^2 + y^2 + z^2 = d^2$$

两边同除以d

$$x \frac {x}{d} + y \frac {y}{d} + z \frac{z}{d} = d$$

$$x * cos ω_x+ y * cos ω_y + z * cos ω_z - d = 0$$

设$$X = { x_1, x_2…x_n}$$为超平面各轴坐标。 $$ω = {cos ω_1, cos ω_2…cos ω_n}$$为法线与各轴夹角的cos值, 于是上式可以写成：

$$\vec{ω} · \vec{X} - d = 0$$ (完)