机器学习-Python 02:线性回归与方差计算
pytho线性回归的示例程序。
# ########################
# 线性回归 #
# 计算、误差估计与偏差评估 #
##########################
# 参考: https://pythonprogramming.net/regression-introduction-machine-learning-tutorial/?completed=/machine-learning-tutorial-python-introduction/
import pandas as pd
import quandl
import numpy as np
from sklearn import preprocessing, svm
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
import math
import matplotlib.pyplot as plt
# 获取goole股票历史数据
df = quandl.get('WIKI/GOOGL') # returns dataframe
# print(df.head())
# 取得其中一部分列
df = df[['Adj. Open', 'Adj. High','Adj. Low','Adj. Close','Adj. Volume', ]]
# High-Low PerCenTage - 计算最高-最低的百分比
df['HL_PCT'] = (df['Adj. High'] - df['Adj. Low']) / df['Adj. Close'] * 100
# open-close percentage change - 计算闭市-开市的增长百分比
df['PCT_change'] = (df['Adj. Close'] - df['Adj. Open']) / df['Adj. Open'] * 100
# 定义新的数据集
df = df[['Adj. Close', 'HL_PCT', 'PCT_change', 'Adj. Volume']]
# 增加一列标签
forecast_col = 'Adj. Close'
# 标记其中的空值
df.fillna(-99999, inplace=True) # fill holes inplace with value -99999
# 取得其中一部分列用于预测
forecast_out = int(math.ceil(0.01*len(df))) # len(df) = 3424
# 将 forecast_col('Adj. Close') 向上移动 #forecast_out 行
# 并赋值给 'label' 列
df['label'] = df[forecast_col].shift(-forecast_out)
# 去除NA的列
df.dropna(inplace=True)
# 定义 X 为特征值, 作为dataframe - 除了label列,
# 然后转换成numpy array
X = np.array(df.drop(['label'],1 ))
# 定义 y 作为对应特征值的标签
y = np.array(df['label'])
# 预处理,即规范化数据。scale X = (X-X_mean)/X_std, 对每个属性/每列来说所有数据都聚集在0附近,方差值为1。
# 参见: https://blog.csdn.net/Dream_angel_Z/article/details/49406573
X = preprocessing.scale(X, axis=0, with_mean=True,with_std=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=-0.2)
# n_jobs : 设置线程数, -1 自动设定
clf = LinearRegression(n_jobs=-1)
# 拟合数据
# 参考: https://ithelp.ithome.com.tw/articles/10206114
clf.fit(X_train, y_train)
accuracy = clf.score(X_test, y_test)
print(accuracy)
#for k in ['linear','poly','rbf','sigmoid']:
# clf = svm.SVR(kernel=k, gamma='scale')
# clf.fit(X_train, y_train)
# confidence = clf.score(X_test, y_test)
# print(k,confidence)
# X 为列,转置为行,便于和y_pred绘制
xfit = np.transpose(X_test)[0]
y_pred = clf.predict(X_test)
# 线性方程的系数
print('Coefficients: \n', clf.coef_)
# 平方差
print("Mean squared error: %.2f" % mean_squared_error(y_test, y_pred))
# Explained variance score 可解释方差: 1 为最佳预测
print('Variance score: %.2f' % r2_score(y_test, y_pred))
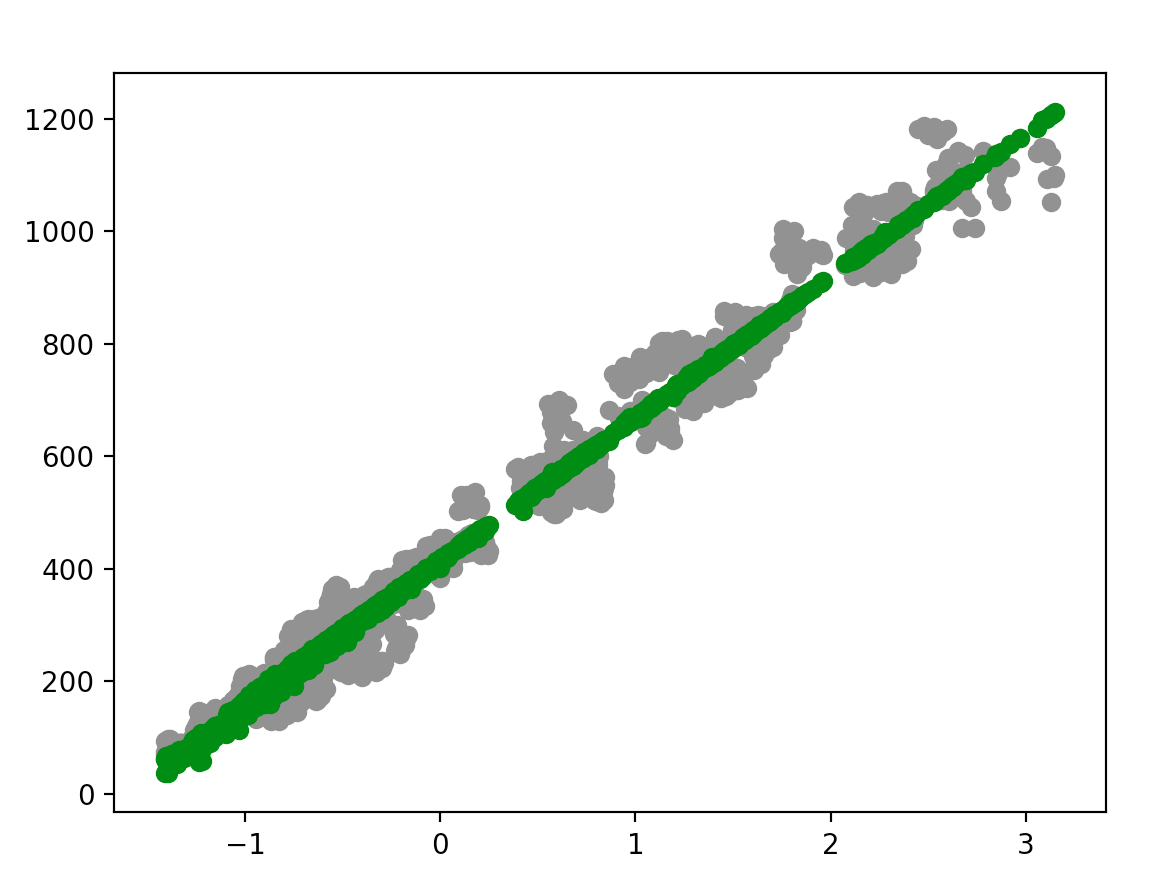
# 画输入点为灰色
plt.scatter(xfit, y_test, color='gray')
# 预测点为绿色
plt.scatter(xfit, y_pred, color='green')
# 显示绘制的图形
plt.show()