向量运算与理解-叉积
叉积的运算、性质、和几何理解
向量点积 $a \cdot b$
$$a \cdot b = ab\,cos\theta$$
$$a \cdot b = \sum_{i=0}^na_ib_i$$
向量内积的几何解释就是一个向量在另一个向量上的投影的积,也就是同方向的积
特别的,如果一个向量如a是某个坐标轴的单位坐标向量,那么,两个向量的点积$a \cdot b$就是向量b在此坐标轴上的坐标值。这个结论非常重要,这是傅立叶分析的理论基础。
其他几何意义:从内积数值上我们可以看出两个向量的在方向上的接近程度。当内积值为正值时,两个向量大致指向相同的方向(方向夹角小于90度);当内积值为负值时,两个向量大致指向相反的方向(方向角大于90度);当内积值为0时,两个向量互相垂直
向量内积的生活解释:单价向量乘以数量向量,得到总价格
向量内积的物理解释:一个斜坡上用力F斜上拉一个物体,位移为S(没有重力的情况下),那么这个力F所作的功
$$W = F_sS = FScos\theta$$
向量叉积 $ a\times b$
叉积$a \times b$是与a 和b都垂直的向量c。其方向由右手定则决定,模长等于以两个向量为边的平行四边形的面积。
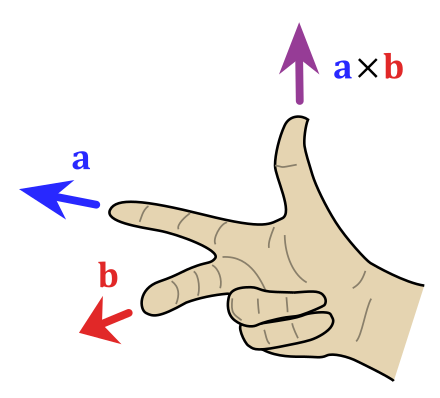
叉积可以定义为:
$$a \times b = \Vert a \Vert \Vert b \Vert sin(\theta) $$
其中$\theta$表示a 和b在它们所定义的平面上的夹角($ 0^\circ \leq \theta \leq 180^\circ $)。$\Vert a \Vert$和$\Vert b \Vert$是向量a和b的模长,而n则是一个与 a、b所构成的平面垂直的单位向量,方向由右手定则决定。
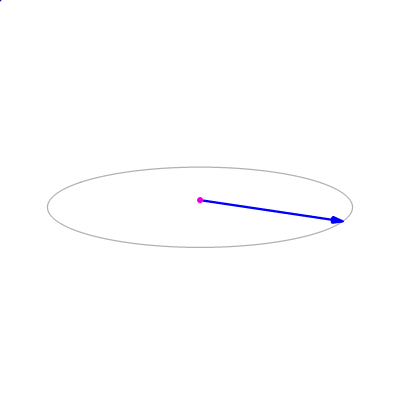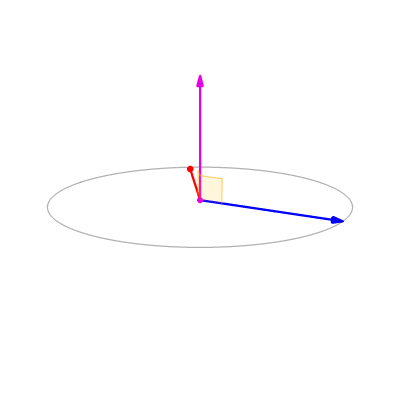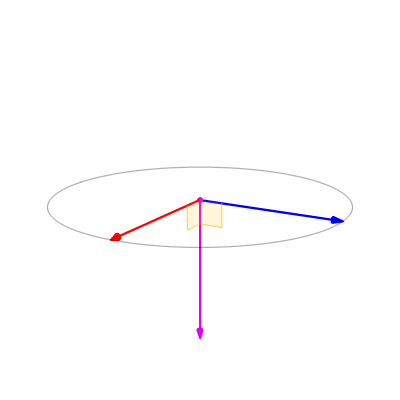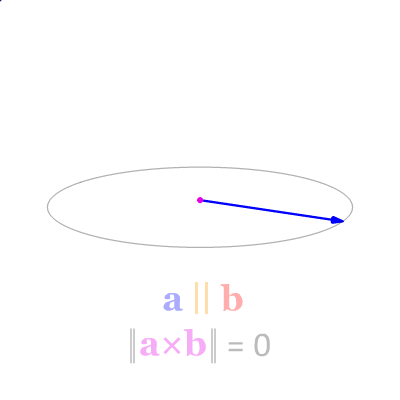
叉积的计算
右手坐标系中,基向量i, j, k满足
$$
i \cdot j = k \\
j \cdot k = i \\
k \cdot i = j
$$
根据反交换律可以得出:
$$
j \cdot i = -k \\
k \cdot j = -i \\
i \cdot k = -j
$$
矩阵表示
$$
u \times v =
\begin{bmatrix}
i & j & k \\
u_1& u_2 & u_3 \\
v_1 & v_2 & v_3
\end{bmatrix}
$$
这个行列式可以使用萨吕法则或拉普拉斯展开计算。使用萨吕法则可以展开为:
根据萨呂法则确定u和v的叉积

使用拉普拉斯展开可以沿第一行展开为:
(参考:维基百科)



